
1.C 2.A 3.B 4.C 5.(1)、(2)、(3)
5、y=±2.解析:由条件易知m=2,n=4.但要注意椭圆焦点所在的坐标轴是y轴.因此准线方程为y=±=±2.
[例题探究]
1, (I)解:设等差数列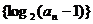 的公差为d.
的公差为d.
由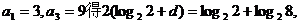 即d=1.
即d=1.
所以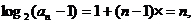 即
即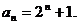
(II)证明因为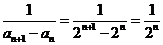 ,
,
所以
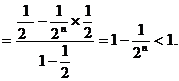
2, 解:(I)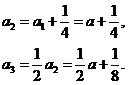
(II) 因为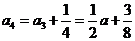 ,所以
,所以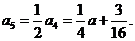
所以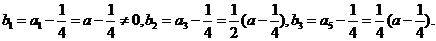
猜想: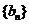 是公比为
是公比为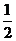 的等比数列.
的等比数列.
证明如下: 因为
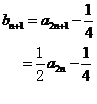
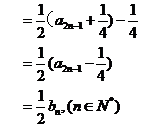
所以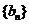 是首项为
是首项为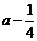 ,公比为
,公比为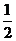 的等比数列.
的等比数列.
3,解:甲方案是等比数列,乙方案是等差数列,
①甲方案获利: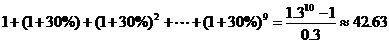 (万元)
(万元)
银行贷款本息: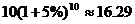 (万元)
(万元)
故甲方案纯利: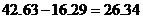 (万元)
(万元)
②乙方案获利: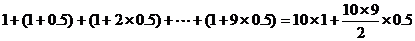
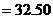 (万元);
(万元);
银行本息和: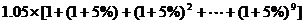
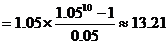 (万元)
(万元)
故乙方案纯利: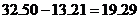 (万元); 综上,甲方案更好.
(万元); 综上,甲方案更好.
冲刺强化训练(14)
1.B 2,A 3,A 4,B
9.设⊙C1,⊙C2,……,⊙Cn是圆心在抛物线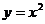 上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为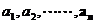 。已知
。已知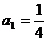 ,
,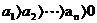 。若⊙Ck (k=1,2,3, ……,n)都与x轴相切,且顺次两圆外切。
。若⊙Ck (k=1,2,3, ……,n)都与x轴相切,且顺次两圆外切。
(1)求证: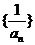 是等差数列 (2)求
是等差数列 (2)求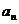 的表达式;
的表达式;
(3)求证: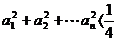
第14讲 等差数列与等比数列
[课前热身]
8.已知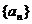 ,
,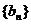 都是各项为正数的数列,对任意的正整n,都有
都是各项为正数的数列,对任意的正整n,都有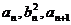 成等差数列,
成等差数列,
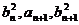 等比数列。
等比数列。
(1)求证: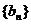 是等差数列;
是等差数列;
(2)如果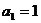 ,
,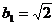 ,
,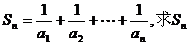 。
。
7.设F是椭圆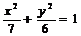 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 (湖南理)
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 (湖南理)
6、在等差数列 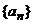 中
中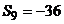 ,
, 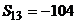 ,等比数列
,等比数列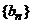 中,
中,
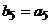 ,
, 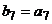 ,则
,则 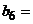
5.设数列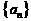 的前
的前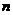 项和为
项和为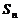 (
(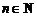 ). 关于数列
). 关于数列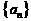 有下列三个命题:
有下列三个命题:
(1)若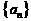 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则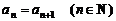 ;
;
(2)若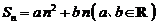 ,则
,则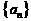 是等差数列;
是等差数列;
(3)若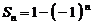 ,则
,则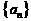 是等比数列.
是等比数列.
这些命题中,真命题的序号是 .
4.在各项都为正数的等比数列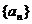 中首项
中首项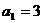 ,前三项和为21,则
,前三项和为21,则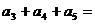 ( )
( )
A.33 B.72 C.84 D.189
3.设数列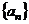 是等差数列,且
是等差数列,且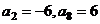 ,
,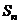 是数列
是数列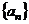 的前
的前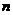 项和,则( )
项和,则( )
A.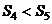 B.
B.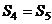 C.
C.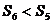 D.
D.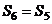
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com