
例8. 已知P是椭圆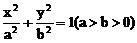 上一点,F1、F2是椭圆的左、右焦点若∠PF1F2=α,∠PF2F1=β,求椭圆离心率。
上一点,F1、F2是椭圆的左、右焦点若∠PF1F2=α,∠PF2F1=β,求椭圆离心率。
解:△PF1F2中,由正弦定理有
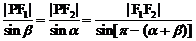
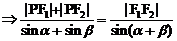
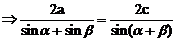
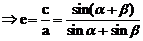
例7. 已知点P是椭圆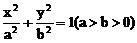 上的一点,F1、F2是两个焦点,且∠F1PF2=α,求△F1PF2的面积S。
上的一点,F1、F2是两个焦点,且∠F1PF2=α,求△F1PF2的面积S。
解:△PF1F2中,由余弦定理,得
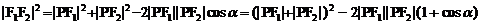
所以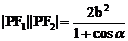
故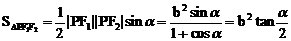
例6. (2002年春季高考题)已知椭圆的焦点是F1、F2,P是椭圆上一个动点,如果延长F1P到Q,使得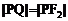 ,那么动点Q的轨迹是( )
,那么动点Q的轨迹是( )
A. 圆 B. 椭圆 C. 双曲线一支 D. 抛物线
解:因为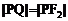 ,所以
,所以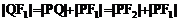
由椭圆第一定义得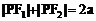 ,故
,故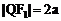 ,即Q点轨迹是以F1为圆心,以2a为半径的圆,选A。
,即Q点轨迹是以F1为圆心,以2a为半径的圆,选A。
例5. (1)(1999年全国联赛题)给定A(-2,2),已知B是椭圆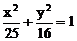 上动点,F是左焦点,当
上动点,F是左焦点,当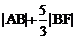 取最小值时,求B点坐标。
取最小值时,求B点坐标。
(2)已知椭圆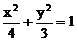 内有一点P(1,-1),F为椭圆右焦点,M是椭圆上动点,求|MP|+|MF|的最小值。
内有一点P(1,-1),F为椭圆右焦点,M是椭圆上动点,求|MP|+|MF|的最小值。
分析:此题如果按一般求最值的方法先建立目标函数,再求最值,因含有两个根式的和,代入消元不易,难以求解,但如果我们注意数量特征,利用椭圆定义合理转化,则可得到如下简解。
解:(1)显然点A在椭圆内部,由椭圆第二定义可得:B到椭圆左准线l的距离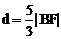 ,所以
,所以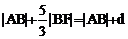 ,结合平面几何知识,可知,当AB⊥l时,
,结合平面几何知识,可知,当AB⊥l时,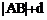 最小,此时易求B点坐标为(
最小,此时易求B点坐标为(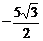 ,2)
,2)
(2)设椭圆的左焦点为F',由平面几何知识,得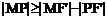 ,当且仅当M为线段F'P的延长线与椭圆交点时取等号。
,当且仅当M为线段F'P的延长线与椭圆交点时取等号。
所以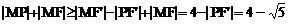
所以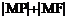 的最小值为
的最小值为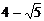 。
。
例3. (2004年高考·全国卷III)设椭圆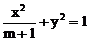 的两个焦点是F1(-c,0)、F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,求m的取值范围。
的两个焦点是F1(-c,0)、F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,求m的取值范围。
解:由题意知m>0,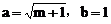 ,
,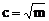 ,且
,且
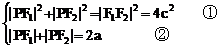
②2-①得:
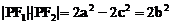
又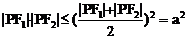
所以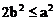 ,即
,即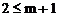 ,所以
,所以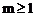
例4. (1997年全国联赛题)若方程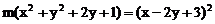 表示的曲线为椭圆,则m的取值范围是( )
表示的曲线为椭圆,则m的取值范围是( )
A. (0,1) B. (1,+∞)
C. (0,5) D. (5,+∞)
分析:由已知得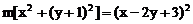
即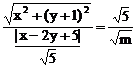
依题意,此方程表示椭圆,根据椭圆的第二定义,得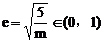 ,解得m>5,选D。
,解得m>5,选D。
例2. 已知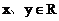 ,且满足
,且满足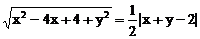 ,试判断点M的轨迹是怎样的曲线。
,试判断点M的轨迹是怎样的曲线。
分析:若将原方程平方,化简后并不能直接判断出轨迹是什么曲线,注意式子结构的特点,左边可看成点M到点(2,0)的距离,从而可联想右边可化为点M到直线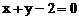 的距离,即有
的距离,即有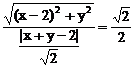 ,由此联想到椭圆的第二定义,就很简单地求出点M的轨迹是椭圆。
,由此联想到椭圆的第二定义,就很简单地求出点M的轨迹是椭圆。
例1. 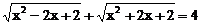
分析:常规方法是经过两次平方去根号求解,但运算繁杂,难免不出错。如果联想到椭圆的第一定义,将方程配方后令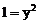 ,得
,得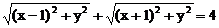 ,则点M(x,y)的轨迹是以F1(-1,0),F2(1,0)为焦点,长轴长为4的椭圆,从而原方程的解等价于已知椭圆上点的纵坐标去求它们的横坐标。
,则点M(x,y)的轨迹是以F1(-1,0),F2(1,0)为焦点,长轴长为4的椭圆,从而原方程的解等价于已知椭圆上点的纵坐标去求它们的横坐标。
解:由原方程可得
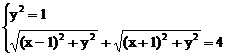
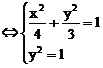
解得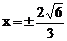
例3 已知cos(α-β)= 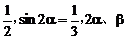 都是锐角,求cos(α+β)的值。
都是锐角,求cos(α+β)的值。
解析:由已知条件有
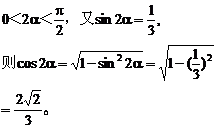
因为0<sin2α=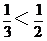 ,
,
所以0<2α<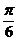 ,
,
所以0<α<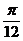 。 ①
。 ①
又因为0<β<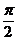 ,
,
所以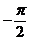 <-β<0 。 ②
<-β<0 。 ②
由①、②得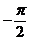 <α-β<
<α-β<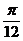 。
。
又因为cos(α-β)=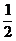 ,
,
所以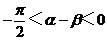 。
。
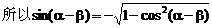
=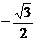 。
。
从而cos(α+β)
=cos[2α-(α-β)]
=cos2αcos(α-β)+sin2αsin(α-β)
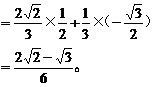
评析:本例通过0<sin2α= 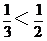 ,发现了隐含条件:0<α<
,发现了隐含条件:0<α<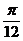 ,将α-β的范围缩小为
,将α-β的范围缩小为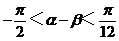 ,进而由cos(α-β)=
,进而由cos(α-β)= 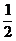 ,将α-β的范围确定为
,将α-β的范围确定为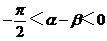 ,从而避免了增解。
,从而避免了增解。
例4 已知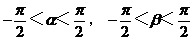 ,且tanα,tnaβ是一元二次方程
,且tanα,tnaβ是一元二次方程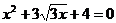 的两个根,求α+β的值。
的两个根,求α+β的值。
解析:由已知条件得tanα+tanβ= 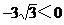 ,
,
tanαtanβ=4>0,
所以tnaα<0,tanβ<0。
又因为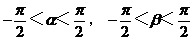 ,
,
所以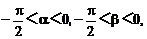
所以-π<α+β<0。
又因为tan(α+β)= 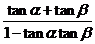
=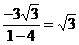
所以α+β= 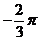 。
。
评析:本例根据韦达定理tanα+tanβ= 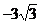 ,tanαtanβ=4,挖掘出了隐含条件tanα<0,tanβ<0,知
,tanαtanβ=4,挖掘出了隐含条件tanα<0,tanβ<0,知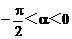 ,
,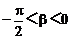 ,得出了α+β的确切范围,从而顺利求解。
,得出了α+β的确切范围,从而顺利求解。
总之,在处理两角和(差)范围问题时,要注意对题目条件加以研究,特别对隐含条件的挖掘,合理选用公式灵活处理。另外涉及多角和(差)的问题,亦可依照上面做法处理。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
例说处理和(差)角范围问题的几点做法 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
例说处理和(差)角范围问题的几点做法 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
周婕 |
一校 |
|
二校 |
|
审核 |
|
||||||
合理选用公式,仅对两角和(差)的范围在相邻两个象限时起作用,而对于其它情形,可通过两角和(差)的两个三角公式,来确定两角和(差)的范围。
例2 已知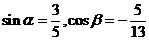 ,且α,β都是第二象限角,试确定2α+β,2α-β所在象限。
,且α,β都是第二象限角,试确定2α+β,2α-β所在象限。
解析:由条件α,β都是第二象限角,则有
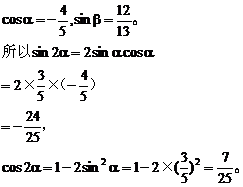
因为2α+β,2α-β都可能落在三个象限,单独使用正(余)弦和差角公式,从值的符号都不能决定2α+β,2α-β的象限,但同时使用正弦、余弦的和差角公式,即可解决。
由cos(2α+β)
=cos2αcosβ-sin2αsinβ
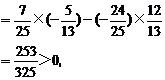
知2α+β在一、四象限。
又sin(2α+β)
=sin2αcosβ+cos2αsinβ
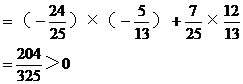
知2α+β在一、二象限。
综上知2α+β在第一象限。
同理可确定2α-β在第三象限。
例1 已知α,β均为锐角, sinα=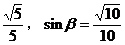 ,求α+β的值。
,求α+β的值。
解析:由已知条件有
cosα=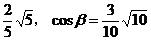 ,且0<α+β<π。
,且0<α+β<π。
又cos(α+β)
=cosαcosβ-sinαsinβ
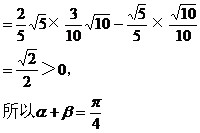
评注:若本题选择正弦的和角公式,会因为一、二象限角的正弦值均为正,而得出两个结果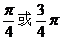 ,导致解题失误,这就需要注意公式的合理选用,若将本例改为:设α是锐角,
,导致解题失误,这就需要注意公式的合理选用,若将本例改为:设α是锐角,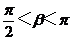 ,且
,且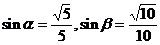 ,求α+β的值,则选用正弦和角公式合理。
,求α+β的值,则选用正弦和角公式合理。
另外,四个象限角的正切值正负相间,故本例亦可选用正切和角公式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com