
2. 深挖隐含
隐含条件是指隐而不显,含而不露的已知条件,它们常常巧妙地隐藏在题目的背后,极易被解题者忽视,从而造成错解或繁解,甚至无法解决。优先考虑隐含条件往往能减少运算量,简化或避免复杂的变化与讨论,找到解题切入点,使问题简捷获解。
例2. 已知x,y是实数,且满足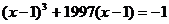 ,
,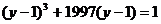 ,则
,则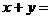 _________。
_________。
分析:按常规思路是解方程分别求出x和y,而x,y无法求出,思维受阻。若观察题目条件,发现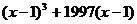 与
与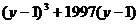 具有对称性。
具有对称性。
若令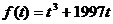 ,则
,则
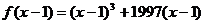 ,
,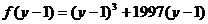 。这样使两方程联系起来。
。这样使两方程联系起来。
解:令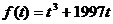
则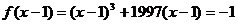
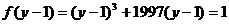
又易知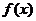 在R上是奇函数,则
在R上是奇函数,则
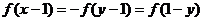 ,又
,又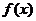 在R上是增函数,故
在R上是增函数,故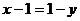 ,即
,即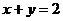 。
。
例3. 解方程组
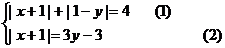
分析:此题按常规方法,需要分四种情况,讨论去掉绝对值符号,然后解方程组。但我们观察(2)式可以挖掘出一个隐含条件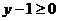 ,利用这个隐含条件可以避免讨论。
,利用这个隐含条件可以避免讨论。
解:由(2)知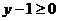 ,(1)式可以变形为
,(1)式可以变形为
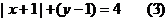
由(2),(3)解得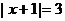
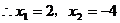 ,分别代入(2)得原方程组的解为
,分别代入(2)得原方程组的解为
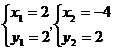
1. 紧扣定义
理解定义、掌握定义、活用定义是解题的一把金钥匙,也是寻找解题切入点的一条重要途径。
例1. 若点M(x,y)满足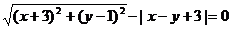 ,则点M的轨迹是( )
,则点M的轨迹是( )
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
解:由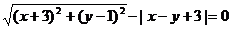 ,
,
得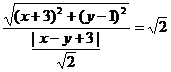
此式可以看成是动点M(x,y)到定点(-3,1)与到定直线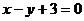 距离之比为
距离之比为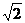 的点的轨迹,根据圆锥曲线的定义,此轨迹为双曲线,故选C。
的点的轨迹,根据圆锥曲线的定义,此轨迹为双曲线,故选C。
注:本题若移项再平方,可进行化简,但表达式中会出现xy项,对曲线的形状的判断有点难度,通过对原式的合理变形,利用圆锥曲线的定义则能很快解决。
将根式转化为能用三角换元法进行换元求值域。
∵函数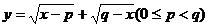 的定义域为
的定义域为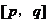 。
。
我们为了将根式转化为能用三角换元法进行换元,使定义域[p,q]与区间[0,1]对应。
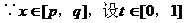
∴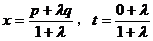 (定比分点坐标公式)
(定比分点坐标公式)
∴消去参数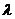 得到
得到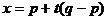 ,将x用t的代数式代入,
,将x用t的代数式代入,
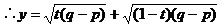
再令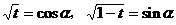
∴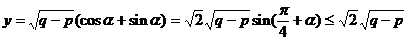
不妨试一试:
(2005年高中联赛题)使关于x的不等式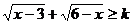 有解的实数k的最大值是D。
有解的实数k的最大值是D。
A. 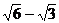 B.
B.
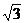 C.
C.
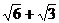 D.
D.
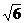
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
关于函数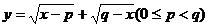 的最大值的求法 的最大值的求法 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
关于函数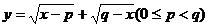 的最大值的求法 的最大值的求法 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
蔡卫琴 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
利用连续函数的可导性
∵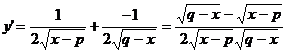
再令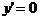 ,解得
,解得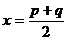
可以证明函数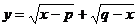 (
(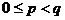 )在(
)在(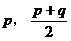 )上是增函数,在
)上是增函数,在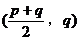 上是减函数。
上是减函数。
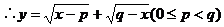 在
在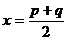 处取得最大值。
处取得最大值。
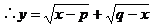 (
(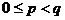 )的最大值为
)的最大值为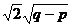 。
。
利用均值不等式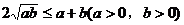
∵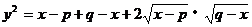
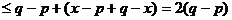
∴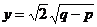
设向量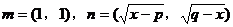 。
。
∵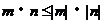
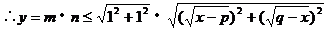
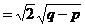
高考命题强调知识之间的交叉、渗透和综合。因此有许多问题可化归于二次函数问题。
例3. 设关于x的一元二次方程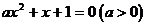 有两个实根
有两个实根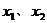 。求证:
。求证: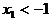 ,且
,且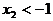 。
。
解析:令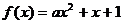
由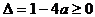 ,得
,得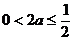
∴函数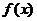 的对称轴
的对称轴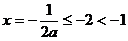
又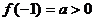 ,所以
,所以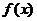 图象与x轴的交点都在点(
图象与x轴的交点都在点(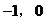 )的左侧,故
)的左侧,故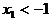 ,且
,且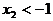 。
。
点评:因此,对于二次函数问题需要掌握解析式、图象和性质的正确使用,选择恰当能使问题轻松解决。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
关于二次函数问题 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
关于二次函数问题 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
李红英 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
二次函数的图象及性质是处理二次函数问题的重要依据,正确地把握图象及性质能使问题轻松解决。
例2. 设函数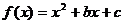 ,方程
,方程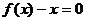 的两实根分别为
的两实根分别为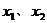 ,且
,且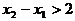 。
。
(1)证明: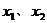 也为方程
也为方程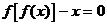 的两根。
的两根。
(2)记四次方程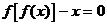 的另两根分别为
的另两根分别为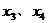 ,且
,且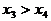 ,试判断
,试判断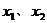 、
、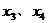 的大小。
的大小。
解析:(1)设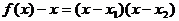 ,则
,则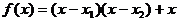
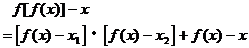
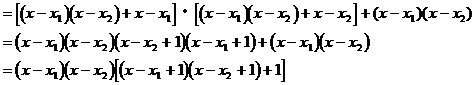
显然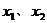 也为方程
也为方程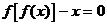 的两根。
的两根。
另外,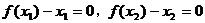
又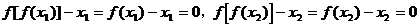
所以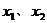 也为
也为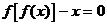 的两根。
的两根。
(2)由(1)知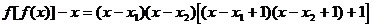 。根据题设知
。根据题设知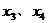 必为方程
必为方程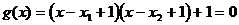 的两根。因
的两根。因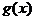 的图象是开口向上的,且
的图象是开口向上的,且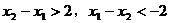 ,得
,得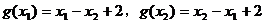 ,所以
,所以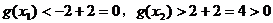 。
。
由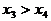 ,根据上述性质可得
,根据上述性质可得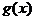 的示意图(如图)。
的示意图(如图)。

由图易知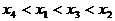 。
。
二次函数的解析式有三种不同形式。①一般式: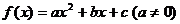 ;②顶点式:
;②顶点式: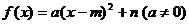 ;③两根式:
;③两根式: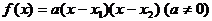 。无论是求解析式,还是运用解析式解决有关问题,都需要根据问题的条件,选取恰当形式。
。无论是求解析式,还是运用解析式解决有关问题,都需要根据问题的条件,选取恰当形式。
例1. 已知函数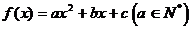 。若
。若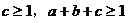 ,且方程
,且方程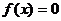 有两个小于1的不等的正根,则a的最小值为( )
有两个小于1的不等的正根,则a的最小值为( )
A. 2 B. 3 C. 4 D. 5
解析:根据题意,设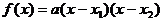 ,其中
,其中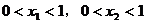 ,且
,且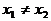 。
。
利用韦达定理得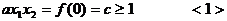
又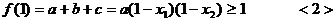
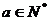 ,由
,由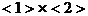 得
得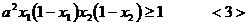
而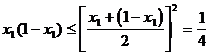 (当且仅当
(当且仅当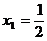 时取等号),
时取等号),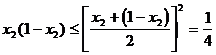 (当且仅当
(当且仅当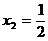 时取等号),通过<3>可得
时取等号),通过<3>可得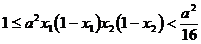 (
(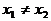 时不等式不能取等号),
时不等式不能取等号),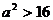 ,即
,即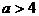 。又
。又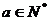 ,a的最小值为5,应选D。
,a的最小值为5,应选D。
例9. (2001年“希望杯”赛题)F1、F2是椭圆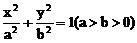 的两个焦点,若椭圆上存在点P使得∠F1PF2=120°,求椭圆离心率的取值范围。
的两个焦点,若椭圆上存在点P使得∠F1PF2=120°,求椭圆离心率的取值范围。
解:由同例8得
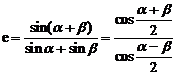
又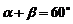 ,所以
,所以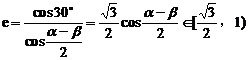
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
例谈椭圆定义在解题中的应用 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
例谈椭圆定义在解题中的应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com