
2. 已知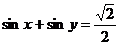 ,求
,求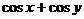 的取值范围。
的取值范围。
1. 已知 ,且
,且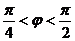 ,求
,求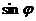 与
与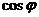 的值。
的值。
3. 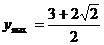 ,
,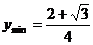
(提示:令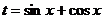 ,则
,则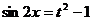 。
。
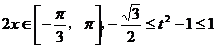 ,
,
解得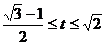 。
。
于是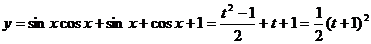 ,容易求解)
,容易求解)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
三角函数求最值的归类研究 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
三角函数求最值的归类研究 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
张玲 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
2. 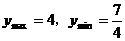
(提示:由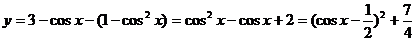 )
)
3. 已知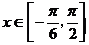 ,求函数
,求函数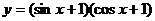 的最大值和最小值。
的最大值和最小值。
答案:1. 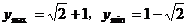
(提示:由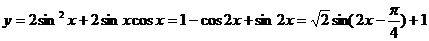 )
)
2. 求函数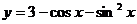 的最大值和最小值。
的最大值和最小值。
例6. 求函数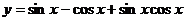 的最大值和最小值。
的最大值和最小值。
解:设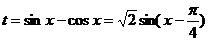 ,
,
则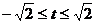 ,且
,且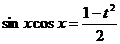 。
。
由于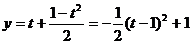 ,
,
故当t=1时,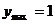 ;当
;当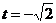 时,
时,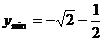 。
。
[点评]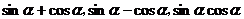 这三者之间有着相互制约,不可分割的密切联系。
这三者之间有着相互制约,不可分割的密切联系。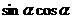 是纽带,三者之间知其一,可求其二。令
是纽带,三者之间知其一,可求其二。令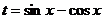 换元后依题意可灵活使用配方法、重要不等式、函数的单调性等方法来求函数的最值。应该注意的是求三角函数的最值方法有多种,像配方法、不等式法等,这里不再赘述,有兴趣的同学不妨自己探讨一下。
换元后依题意可灵活使用配方法、重要不等式、函数的单调性等方法来求函数的最值。应该注意的是求三角函数的最值方法有多种,像配方法、不等式法等,这里不再赘述,有兴趣的同学不妨自己探讨一下。
练一练:
1. 求函数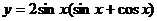 的最大值和最小值。
的最大值和最小值。
例5. 求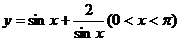 的最小值。
的最小值。
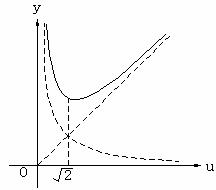
解:设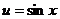 ,则
,则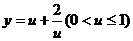 。
。
从图2中可以看到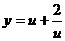 在区间
在区间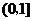 上是减函数(也可以利用函数的单调性定义来证明这一结论)。
上是减函数(也可以利用函数的单调性定义来证明这一结论)。
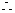 当
当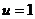 时,
时,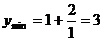
[点评]若由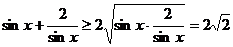 ,可得最小值
,可得最小值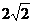 是错误的。
是错误的。
这是因为当等号成立时,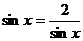 ,
,
即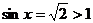 是不可能的。若把此题改为
是不可能的。若把此题改为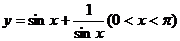 就可以用不等式法求解了,同学们不妨琢磨一下。
就可以用不等式法求解了,同学们不妨琢磨一下。
例4. 求函数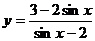 的最大值和最小值。
的最大值和最小值。
解: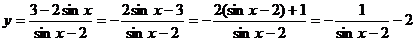
由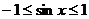 ,得
,得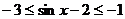 ,
,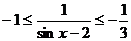 ,
,
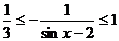 ,即
,即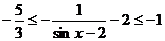
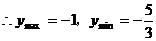
[点评]此题是利用了分离分母的方法求解的。若用例3的解法同样可求,有兴趣的同学不妨试一下,并作解法对比。
例3. 求函数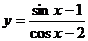 的最大值和最小值。
的最大值和最小值。
解:由已知得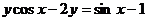 ,
,
即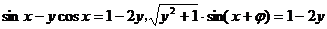 ,
,
所以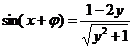
因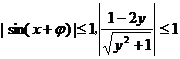 ,
,
即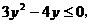 解得
解得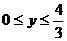 ,
,
故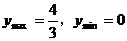
[点评]上述利用正(余)弦函数的有界性,转化为以函数y为主元的不等式,是解决这类问题的最佳方法。虽然本题可以使用万能公式,也可以利用圆的参数方程和斜率公式去求解,但都不如上述解法简单易行。有兴趣的同学不妨试一试其他解法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com