
把数化为形是“数形结合”思想。利用图形的直观性化难为易,有事半功倍之效,简洁明快之感。
1. 求函数值域。
例4. 求函数 的值域。
的值域。
解:由图10知函数的值域为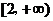 。
。
分段函数作图法是把原函数等价转化为分段函数后再作图,这种方法是画含有绝对值的函数的图象的有效方法。
例3. 作出下列函数的图象。
(1)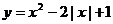 ;(2)
;(2) ;(3)
;(3) 。
。
解:(1)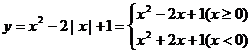
图9就是所要画的函数图象。
(2)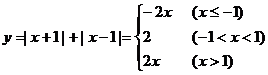
图10就是所要画的函数图象。
(3)
图11就是所要画的函数图象。
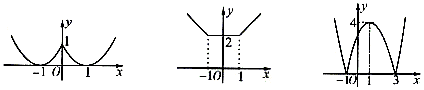
图9 图10 图11
注:分段函数作图法是画含绝对值函数的图象的常规之法。三点作图法、翻转作图法虽然简便,但要注意适应的题型,第(3)小题也可用翻转作图法,有兴趣的同学不妨试一试。
翻转作图法是画函数 的图象的一种简捷方法。
的图象的一种简捷方法。
步骤是:①先作出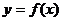 的图象;②若
的图象;②若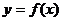 的图象不位于x轴下方,则函数
的图象不位于x轴下方,则函数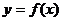 的图象就是函数
的图象就是函数 的图象;③若函数
的图象;③若函数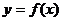 的图象有位于x轴下方的,则可把x轴下方的图象绕x轴翻转180°到x轴上方,就得到了函数
的图象有位于x轴下方的,则可把x轴下方的图象绕x轴翻转180°到x轴上方,就得到了函数 的图象。
的图象。
例2. 作出下列各函数的图象。
(1)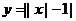 ;(2)
;(2) ;(3)
;(3)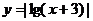 。
。
解:(1)先作出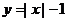 的图象,如图3,把图3中x轴下方的图象翻上去,得到图4。图4就是要画的函数图象。
的图象,如图3,把图3中x轴下方的图象翻上去,得到图4。图4就是要画的函数图象。
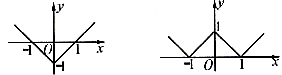
图3 图4
(2)先作出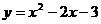 的图象,如图5。把图5中x轴下方的图象翻上去,得到图6。图6就是要画的函数图象。
的图象,如图5。把图5中x轴下方的图象翻上去,得到图6。图6就是要画的函数图象。

图5 图6
(3)先作出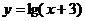 的图象,如图7。把图7中x轴下方的图象翻上去,得到图8。图8就是要画的函数图象。
的图象,如图7。把图7中x轴下方的图象翻上去,得到图8。图8就是要画的函数图象。

图6 图7
三点作图法是画函数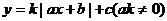 的图象的一种简捷方法(该函数图形形状似“V”,故称V型图)。
的图象的一种简捷方法(该函数图形形状似“V”,故称V型图)。
步骤是:①先画出V型图顶点 ;
;
②在顶点两侧各找出一点;
③以顶点为端点分别与另两个点画两条射线,就得到函数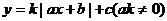 的图象。
的图象。
例1. 作出下列各函数的图象。
(1)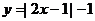 ;(2)
;(2) 。
。
解:(1)顶点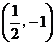 ,两点(0,0),(1,0)。其图象如图1所示。
,两点(0,0),(1,0)。其图象如图1所示。
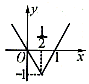
图1
(2)顶点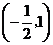 ,两点(-1,0),(0,0)。其图象如图2所示。
,两点(-1,0),(0,0)。其图象如图2所示。

图2
注:当k>0时图象开口向上,当k<0时图象开口向下。函数图象关于直线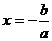 对称。
对称。
1. 分类讨论。2. 变换主元。3. 数形结合。4. 分离参数。5. 最值性质:(1) 恒成立
恒成立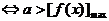 ;(2)
;(2) 恒成立
恒成立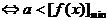 ;(3)
;(3) 有解
有解 ;(4)
;(4) 有解
有解 。
。
例1. 解关于x的不等式: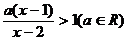 。
。
解析:该不等式的基本类型为分式不等式,应通过移项→通分→调整系数→数轴标根等步骤完成,但在调整系数及数轴标根时,涉及到对参数a的分类讨论。分类时,应当根据条件正确制定分类标准,确保所有可能情形都考虑到。做到不重不漏。
(1)当a≠1时,原不等式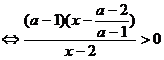 。
。
①当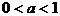 时,解为
时,解为 ;
;
②当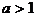 时,解为
时,解为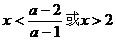 ;
;
③当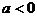 时,解为
时,解为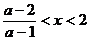
④当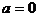 时,无解。
时,无解。
(2)当a=1时,解为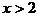 。
。
例2. 若不等式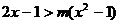 对满足
对满足 的所有实数m都成立,求x的取值范围。
的所有实数m都成立,求x的取值范围。
解析:已知参数m的取值范围而求未知数x的取值范围,可采用变换主元的策略,原不等式可变形为 ,当
,当 时恒成立。构造以m为自变量的函数
时恒成立。构造以m为自变量的函数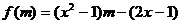 ,则原问题可等价转化为函数
,则原问题可等价转化为函数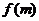 在区间[-2,2]上的函数值恒小于零,从而有
在区间[-2,2]上的函数值恒小于零,从而有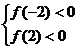 ,即
,即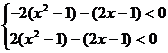 ,
,
解得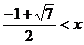
 。
。
例3. 已知对任意实数x,不等式 恒成立。求实数k的取值范围。
恒成立。求实数k的取值范围。
解:原不等式两端可视为两个函数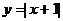 与y=kx,在同一坐标系中画出这两个函数的图象,问题的解决方法自然产生。如图,只有当直线
与y=kx,在同一坐标系中画出这两个函数的图象,问题的解决方法自然产生。如图,只有当直线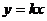 的斜率k取区间[0,1]上的任一值时,才有
的斜率k取区间[0,1]上的任一值时,才有 恒成立。故实数k的取值范围为
恒成立。故实数k的取值范围为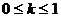 。
。
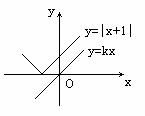
例4. 函数 为定义在
为定义在 上的增函数。
上的增函数。
若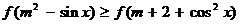 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
解:依题意,原不等式
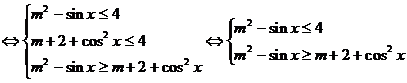
对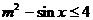 分离参数m,应用得:
分离参数m,应用得:
 在函数定义域中恒成立
在函数定义域中恒成立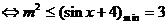 ,
,
可得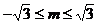
对 分离参数m,应用得:
分离参数m,应用得:
 对一切
对一切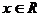 恒成立
恒成立
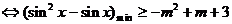 。
。
可得
由①、②可知,实数m的取值范围为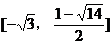 。
。
[练一练]
求使不等式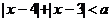 有解的实数a的取值范围。
有解的实数a的取值范围。
答案: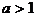 。
。
提示:只需求出 的最小值,只要a大于其最小值即可,求出坐标轴上到两点和的最小值。
的最小值,只要a大于其最小值即可,求出坐标轴上到两点和的最小值。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
参数不等式问题优解例析 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
参数不等式问题优解例析 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
蔡卫琴 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例4 (1998年高考理)设曲线C的方程是 ,将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C1
,将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C1
(I)写出曲线C1的方程;
(II)证明曲线C与C1关于 点对称;
点对称;
(I)解:曲线C1的方程为:
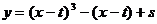
(II)证明:在曲线C上任取一点B1(x1,y1)。设B2(x2,y2)是B1关于点A的对称点,则有:
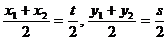
所以
代入曲线C的方程,得x2和y2满足方程:
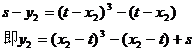
可知点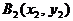 在曲线C1上
在曲线C1上
反过来,同样可以证明,在曲线C1上的点关于点A的对称点在曲线C上。因此,曲线C与C1关于点A对称。
例5 (1997年高考文)椭圆C与椭圆C1: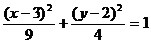 关于直线
关于直线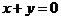 对称,椭圆C的方程是( )
对称,椭圆C的方程是( )
A. 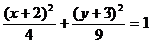 B.
B. 
C. 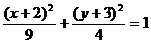 D.
D. 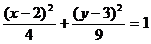
解:设(x,y)是椭圆C上任意一点,则其关于直线 的对称点可求得为
的对称点可求得为 ,该点在椭圆C1上,故其坐标适合椭圆C1的方程,将其代入有:
,该点在椭圆C1上,故其坐标适合椭圆C1的方程,将其代入有: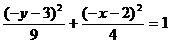 ,化简后知选A。
,化简后知选A。
从以上几个方面的研究可以发现,相关点法是解决数学对称问题的有效方法,因为它抓住了图象对称的基本元素(即图象上点与点之间的一一对应的对称关系)和核心,并且将几何问题代数化的基本数学思想得到很好地体现运用。此外,相关点法在解决几何中才被得以提出并加以运用于解决对称问题,这一点从例4,例5可以感觉到,实际上,函数及三角函数中的对称与解析几何中的对称是相通的,因此,相关点法完全可以加以推广,实行方法共享。
哈尔滨师范大学(150080)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
利用相关点法巧解对称问题 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
利用相关点法巧解对称问题 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
尤新建 |
审稿老师 |
|
||||||||||
|
录入 |
李金颖 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例3 (2003年高考江苏卷)已知函数 是R上的偶函数,其图象关于点
是R上的偶函数,其图象关于点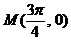 对称,且在区间
对称,且在区间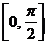 上是单调函数,求
上是单调函数,求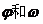 的值。
的值。
解:由 是偶函数,得
是偶函数,得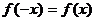
即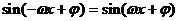
所以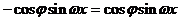
对任意x都成立,且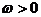 ,所以得
,所以得

依题设 ,所以解得
,所以解得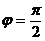 ,这时
,这时
由 的图象关于点M对称,可设P(x,y)是其图象上任意一点,P点关于
的图象关于点M对称,可设P(x,y)是其图象上任意一点,P点关于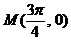 的对称点可求得为:
的对称点可求得为:
即有 ,(*)
,(*)
取x=0,得 ,所以,
,所以,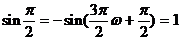
所以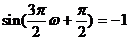
所以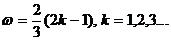
当 时,
时, 上是减函数;
上是减函数;
当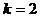 时,
时, 在
在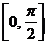 上是减函数;
上是减函数;
当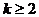 时,
时,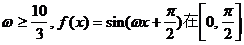 上不是单调函数;
上不是单调函数;
所以,综合得
评注:本题是三角函数中含有中心对称问题,抓住对称点之间的中心对称关系,利用中点坐标公式求出对称点(或称相关点),寻求两相关点(对称点)之间的函数等量关系(见*)是解决问题的关键。
例1 (2001年高考)设 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线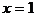 对称。证明
对称。证明 是周期函数。
是周期函数。
证明:设(x,y)为 图象上任意一点,则其关于
图象上任意一点,则其关于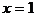 的对称点可求得:
的对称点可求得: ,于是根据函数关系有:
,于是根据函数关系有: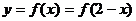 ,又因为
,又因为 是定义在R上的偶函数,故有:
是定义在R上的偶函数,故有: ,因此结合上式有:
,因此结合上式有: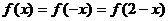 ,故由
,故由 知:
知: 是周期函数,
是周期函数,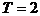 。
。
例2 (1997年高考文)设 是定义在R上的函数,则函数
是定义在R上的函数,则函数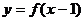 与
与 的图象关于( )
的图象关于( )
A. 直线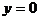 对称 B. 直线
对称 B. 直线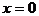 对称
对称
C. 直线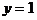 对称 D. 直线
对称 D. 直线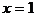 对称
对称
解:可设(x1,y)为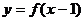 上任意一点,则有
上任意一点,则有 ;
;
若(x2,y)为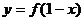 上一点,也有
上一点,也有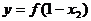 ,一般地,由
,一般地,由
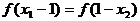 可知:
可知: ,所以
,所以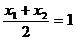 ,即(x1,y)与(x2,y)关于直线
,即(x1,y)与(x2,y)关于直线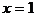 对称,故选(D)。
对称,故选(D)。
评注:例1是一个函数图象本身内在对称问题,例2是两个函数图象之间的对称问题,尽管问题情境不同,但解法有相通之处,均可抓住对称点(即相关点)加以讨论。
3. 函数对称性应用举例
例1 定义在R上的非常数函数满足: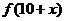 为偶函数,且
为偶函数,且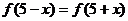 ,则
,则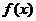 一定是( )
一定是( )
A. 是偶函数,也是周期函数
B. 是偶函数,但不是周期函数
C. 是奇函数,也是周期函数
D. 是奇函数,但不是周期函数
解:因为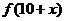 为偶函数,所以
为偶函数,所以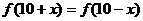 。
。
所以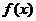 有两条对称轴
有两条对称轴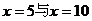 ,因此
,因此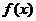 是以10为其一个周期的周期函数,所以x=0即y轴也是
是以10为其一个周期的周期函数,所以x=0即y轴也是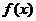 的对称轴,因此
的对称轴,因此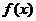 还是一个偶函数。故选(A)。
还是一个偶函数。故选(A)。
例2 设定义域为R的函数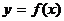 、
、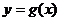 都有反函数,并且
都有反函数,并且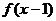 和
和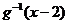 的函数图像关于直线
的函数图像关于直线 对称,若
对称,若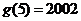 ,那么
,那么 ( )
( )
A. 2002 B. 2003 C. 2004 D. 2005
解:因为 的函数图像关于直线
的函数图像关于直线 对称,所以
对称,所以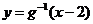 的反函数是
的反函数是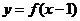 ,而
,而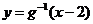 的反函数是
的反函数是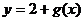 ,所以
,所以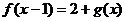 ,所以有
,所以有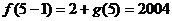
故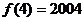 ,应选(C)。
,应选(C)。
例3 设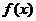 是定义在R上的偶函数,且
是定义在R上的偶函数,且 ,当
,当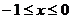 时,
时, ,则
,则 ___________
___________
解:因为f(x)是定义在R上的偶函数,所以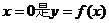 的对称轴;
的对称轴;
又因为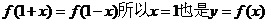 的对称轴。故
的对称轴。故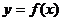 是以2为周期的周期函数,所以
是以2为周期的周期函数,所以
例4 函数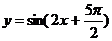 的图像的一条对称轴的方程是( )
的图像的一条对称轴的方程是( )
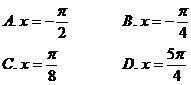
解:函数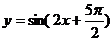 的图像的所有对称轴的方程是
的图像的所有对称轴的方程是 ,所以
,所以 ,显然取
,显然取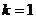 时的对称轴方程是
时的对称轴方程是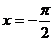 ,故选(A)。
,故选(A)。
例5 设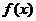 是定义在R上的奇函数,且
是定义在R上的奇函数,且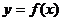 的图象关于直线
的图象关于直线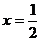 ,则:
,则: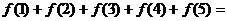 _____________
_____________
解:函数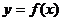 的图像既关于原点对称,又关于直线
的图像既关于原点对称,又关于直线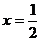 对称,所以周期是2,又
对称,所以周期是2,又 ,图像关于
,图像关于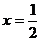 对称,所以
对称,所以 ,所以
,所以
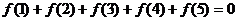
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
函数对称性的探究 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
函数对称性的探究 |
栏目名称 |
学法指导 |
||||||||||
|
供稿老师 |
|
辅导老师 |
|
||||||||||
|
录入 |
李金颖 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
2. 不同函数对称性的探究
定理4 函数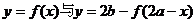 的图像关于点
的图像关于点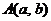 成中心对称。
成中心对称。
证明:设点 图像上任一点,则
图像上任一点,则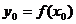 。点
。点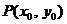 关于点
关于点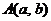 的对称点为
的对称点为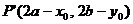 ,此点坐标满足
,此点坐标满足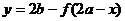 ,显然点
,显然点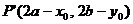 在
在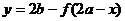 的图像上。
的图像上。
同理可证: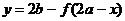 图像上关于点
图像上关于点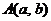 对称的点也在
对称的点也在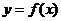 的图像上。
的图像上。
推论 函数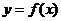 与
与 的图像关于原点成中心对称。
的图像关于原点成中心对称。
定理5 函数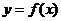 与
与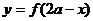 的图像关于直线
的图像关于直线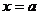 成轴对称。
成轴对称。
证明 设点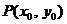 是
是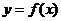 图像上任意一点,则
图像上任意一点,则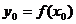 。点
。点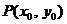 关于直线
关于直线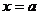 的对称点为
的对称点为 ,显然点
,显然点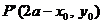 在
在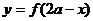 的图像上。
的图像上。
同理可证: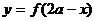 图像上关于直线
图像上关于直线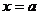 对称的点也在
对称的点也在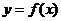 图像上。
图像上。
推论 函数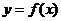 与
与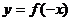 的图像关于直线y轴对称。
的图像关于直线y轴对称。
定理6 ①函数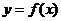 与
与 的图像关于直线
的图像关于直线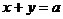 成轴对称。
成轴对称。
②函数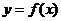 与
与 的图像关于直线
的图像关于直线 成轴对称。
成轴对称。
现证定理6中的②
设点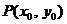 是
是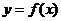 图像上任一点,则
图像上任一点,则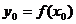 。记点
。记点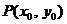 关于直线
关于直线 的对称点
的对称点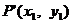 ,则
,则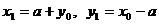 ,所以
,所以
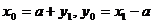 代入
代入
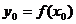 之中得
之中得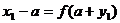 。所以点
。所以点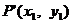 在函数
在函数 的图像上。
的图像上。
同理可证:函数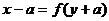 的图像上任一点关于直线
的图像上任一点关于直线 的轴对称点也在函数
的轴对称点也在函数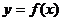 的图像上。故定理6中的②成立。
的图像上。故定理6中的②成立。
推论 函数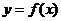 的图像与
的图像与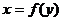 的图像关于直线
的图像关于直线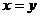 成轴对称。
成轴对称。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com