
21. (本小题满分12分)
关于用二分法求函数零点的近似值,完成下面的填空。
(I)完成下面用二分法求函数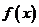 的零点近似值的步骤;
的零点近似值的步骤;
第一步,确定区间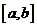 ,验证
,给定精度
,验证
,给定精度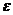 ;
;
第二步,求区间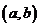 的中点
的中点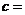 ;
;
第三步,计算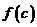 ,并做如下处理:
,并做如下处理:
(1)若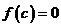 ,则
就是
,则
就是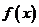 的零点;
的零点;
(2)若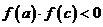 ,则令
;
,则令
;
(3)若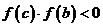 ,则令
。
,则令
。
第四步,判断是否达到精度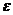 :即若
:即若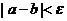 ,则得到零点的近似值
,则得到零点的近似值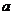 (或
(或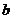 );
);
否则,重复 。
(II)若用“二分法”求方程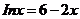 的近似解,则
的近似解,则
(1)方程的根所在的区间是 ;
供选择的区间为: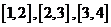
(2)把(1)中选定的区间对分一次,可以得出方程的根所在的区间为 ;
(3)对(1)中选定的区间,如果精度为0.1,那么,至多要对分区间 次。
20. (本小题满分12分)
如图,在正方体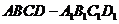 中,
中,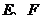 分别为棱
分别为棱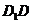 和
和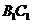 的中点。
的中点。
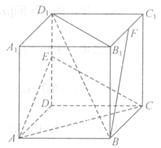 (I)求证:
(I)求证: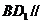 平面
平面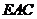 ;
;
(II)求证:平面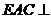 平面
平面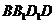 ;
;
(III)求直线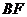 与平面
与平面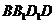 多成角的正弦值。
多成角的正弦值。
19. (本小题满分12分)
某工厂生产一种低碳燃料,每月的固定成本为20万元,可变成本为2000元/吨。经市场调查发现,该染料的月销售量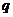 (单位:吨)和销售单价
(单位:吨)和销售单价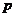 (单位:元/吨)之间的函数关系是:
(单位:元/吨)之间的函数关系是: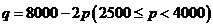 。如果每月生产的染料都能售出,那么,单价定为多少时,才能获得最大利润?最大利润是多少?
。如果每月生产的染料都能售出,那么,单价定为多少时,才能获得最大利润?最大利润是多少?
注:利润=销售收入-总成本;总成本=不变成本+可变成本
18. (本小题满分12分)
 函数
函数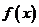 是定义在
是定义在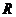 上的奇函数,当
上的奇函数,当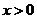 时,
时,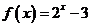 。
。
(I)求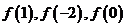 ;
;
(II)求函数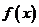 的解析式;
的解析式;
(III)画出函数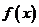 的草图,写出函数的单调区间并指出单调性。
的草图,写出函数的单调区间并指出单调性。
17. (本小题满分10分)
已知直线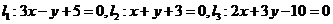 。
。
(I)求过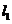 和
和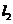 交点且与
交点且与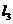 平行的直线方程;
平行的直线方程;
(II)求过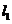 个
个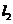 交点且与
交点且与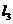 垂直的直线方程。
垂直的直线方程。
16.已知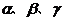 为平面,
为平面,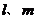 为直线,在下面五组条
为直线,在下面五组条
件中:
①存在无数条直线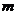 ,满足
,满足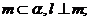 ②
②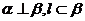 ;③
;③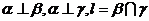 ;④
;④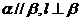 ;⑤
;⑤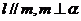 。
。
其中能够判定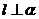 成立的为
。(写出所有正确选项的序号)
成立的为
。(写出所有正确选项的序号)
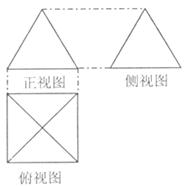
15. 一个几何体的正视图和侧视图都是边长为2的等边三
角形,俯视图如图所示,则giant几何体的表面积
为 。
14. 已知函数
已知函数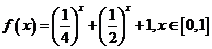 ,则
,则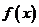
的最大值为 。
13.点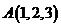 和
和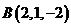 是空间直角坐标系
是空间直角坐标系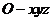 中的点,点
中的点,点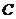 和点
和点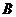 关于平面
关于平面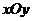 对称,则
对称,则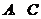 两点间的距离为
。
两点间的距离为
。
12. 若直线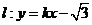 与直线
与直线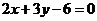 的交点位于第一象限,则直线
的交点位于第一象限,则直线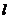 的倾斜角
的倾斜角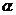 的范围是
的范围是
A、0°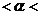 30°
B、30°
30°
B、30° 90°
90°
C、60°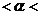 90°
D、60°
90°
D、60°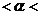 180°
180°
第II卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com