
19. (本小题满分12分)
已知四棱锥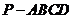 的底面
的底面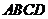 是菱形;
是菱形;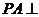 平面
平面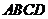 ,
,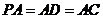 ,
,
点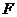 为
为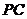 的中点.
的中点.
(Ⅰ)求证: 平面
平面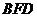 ;
;
(Ⅱ)求二面角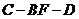 的正切值.
的正切值.
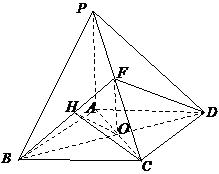 (Ⅰ)证明: 连结
(Ⅰ)证明: 连结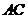 ,
,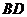 与
与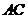 交于点
交于点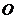 ,连结
,连结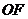 .
. 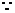
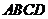 是菱形, ∴
是菱形, ∴ 是
是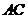 的中点.
的中点.  点
点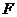 为
为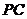 的中点, ∴
的中点, ∴ .
. 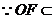 平面
平面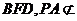 平面
平面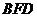 , ∴
, ∴ 平面
平面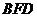 .
.
(Ⅱ)解法一:
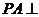 平面
平面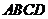 ,
,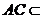 平面
平面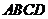 ,∴
,∴ 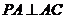 .
.
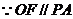 ,∴
,∴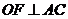 .
. 
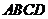 是菱形, ∴
是菱形, ∴ .
.
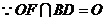 ,
,
∴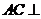 平面
平面 .
.
作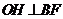 ,垂足为
,垂足为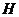 ,连接
,连接 ,则
,则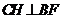 ,
,
所以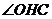 为二面角
为二面角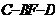 的平面角.
的平面角.
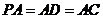 ,∴
,∴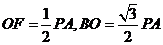 ,
,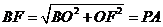 .
.
在Rt△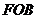 中,
中,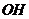 =
=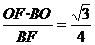
 ,∴
,∴
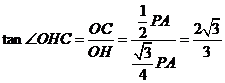 .
.
∴二面角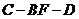 的正切值为
的正切值为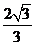
 .
.
解法二:如图,以点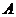 为坐标原点,线段
为坐标原点,线段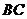 的垂直平分线所在直线为
的垂直平分线所在直线为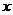 轴,
轴,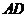 所在直线为
所在直线为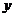 轴,
轴,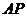 所在直线为
所在直线为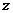 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令 ,
,
则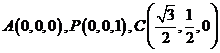 ,
,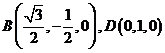 ,
, .
.
∴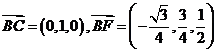 .设平面
.设平面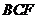 的一个法向量为
的一个法向量为
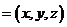 ,
,
由
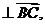

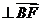 ,得
,得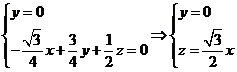 ,
,
 令
令 ,则
,则 ,∴
,∴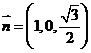 .
.
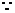
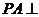 平面
平面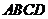 ,
,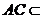 平面
平面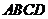 ,
,
∴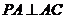 .
.
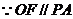 ,∴
,∴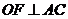 .
.
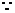
 是菱形,∴
是菱形,∴ .
.
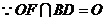 ,∴
,∴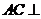 平面
平面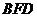 .
.
∴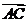 是平面
是平面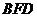 的一个法向量,
的一个法向量,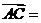
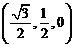 .
.
∴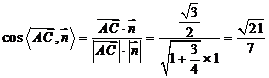 ,
,
∴ ,∴
,∴ . 13分
. 13分
∴二面角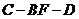 的正切值为
的正切值为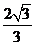 .
.
18.(本小题满分12分)
“ 五·一”黄金周某旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条旅游线路.
(Ⅰ)求3个旅游团选择3条不同的线路的概率;
(Ⅱ)求恰有2条线路被选择的概率.
解:(Ⅰ)3个旅游团选择3条不同线路的概率为P1=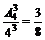
(Ⅱ)恰有两条线路被选择的概率为P2=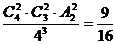
另解:恰有一条线路被选择的概率为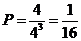
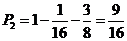

17.(本小题满分10分)
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
|
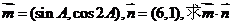
 的最大值。
的最大值。
(I)∵(2a-c)cosB=bcosC,∴(2sinA-sinC)cosB=sinBcosC
即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA.∵0<A<π,∴sinA≠0. ∴cosB=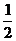 .
.
∵0<B<π,∴B= .
.
(II)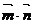 =6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,
=6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,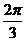 )设sinA=t,则t∈
)设sinA=t,则t∈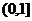 .
.
则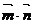 =-2t2+6t+1=-2(t-
=-2t2+6t+1=-2(t-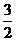 )2+
)2+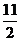 ,t∈
,t∈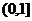 .∴t=1时,
.∴t=1时,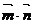 取最大值.5
取最大值.5
16.已知双曲线 的右顶点到其渐近线的距离不大于
的右顶点到其渐近线的距离不大于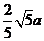 ,其离心率e的取值范围为____(1,
,其离心率e的取值范围为____(1,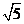 ]
]
15.△ABC的三边长为1,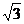 ,2,P 为平面ABC外一点,它到三顶点的距离都等于2,则P到平面ABC的距离为___
,2,P 为平面ABC外一点,它到三顶点的距离都等于2,则P到平面ABC的距离为___ ____.
____.
14. 若二项式(x+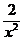 )n的展开式共7项,则展开式中的常数项为_____60__.
)n的展开式共7项,则展开式中的常数项为_____60__.
13.不等式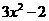 ﹥︱x︱
﹥︱x︱ 的解集为
的解集为 __{x|x﹤-1或x﹥1}________
__{x|x﹤-1或x﹥1}________
12.16.已知方程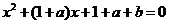 的两个实根
的两个实根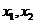 ,满足0﹤
,满足0﹤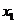 ﹤1﹤
﹤1﹤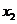 ,则
,则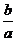 的取值范围是( C )
的取值范围是( C )
A.(-2,0) B.(0,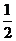 ) C.
) C.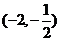 D.(
D.(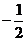 ,0)
,0)
10.函数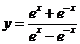 的图像大
的图像大 致为
( A ).
致为
( A ).

11直线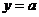 与函数
与函数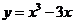 的图象有相异三个交点,则
的图象有相异三个交点,则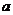 的取值范围是(
A )
的取值范围是(
A )
A.(-2,2) B.(-2,0) C.(0,2) D.(2,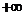 )
)
9.数列{an}中a3=2,a7=1,如果数列{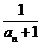 }是等差数列,那么a11=
( S)
}是等差数列,那么a11=
( S)
A.0 B.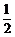 C.
C.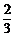 D.1
D.1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com