
可取n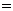
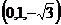
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
及n?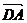
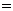
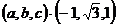
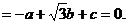
则由n?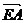
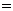
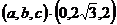
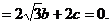
设平面ADE的法向量为n=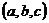 ,
,
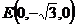
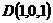 ,
,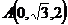
则由已知条件有: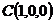 ,
,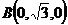 ,
,
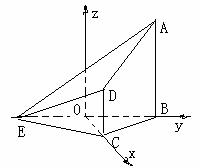 解法1:取BE的中点O,连OC.
解法1:取BE的中点O,连OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O-xyz如图,
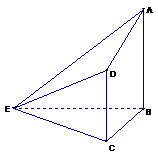 6. 〖理科、文科〗如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD= 2, ∠BCE=1200.
6. 〖理科、文科〗如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD= 2, ∠BCE=1200.
(Ⅰ)求证:平面ADE⊥平面ABE ;
(Ⅱ)求点C到平面ADE的距离.
 点
点 到平面
到平面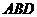 的距离
的距离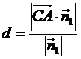
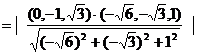 =
=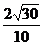 .
.
注:若为了看图方便,也可以把图调整后,标好字母证明之.
(Ⅲ)解法3:由(Ⅱ)解法2,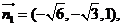
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com