
从而点C到平面ADE的距离为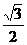
由已知有AB⊥BE.
BE=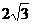 ,AB= 2, ∴BH=
,AB= 2, ∴BH=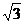 ,
,
点C到平面ADE的距离等于点B到平面ADE的距离的 .
.
过B作BH⊥AE,垂足为H.∵平面ADE.⊥平面ABE.∴BH⊥平面BDE.
(Ⅱ)∵CD 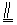
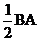 ,延长AD, BC交于T
,延长AD, BC交于T
则C为BT的中点.
∴CD 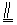
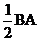 ,
,
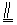 CD∴
CD∴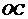 ∥ FD
∥ FD
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.
 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
解法2:取BE的中点O,AE的中点F,连OC,OF,DF.则
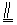
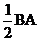
(Ⅱ)点C到平面ADE的距离为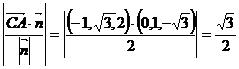
∵n?m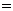
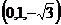 ?
?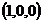 =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE.
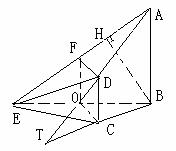
∴平面ABE的法向量可取为m=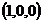 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com