1、定义运算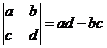，则符合条件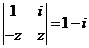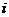（为虚数单位）的复数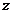为（    ）

于是 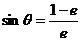，为所求．…………………………………………………………14分

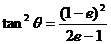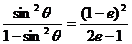将 c = ea代入，得 Û  Û ，

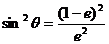将x₀、y₀代入上式，得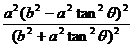++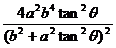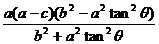= ac．去分母，整理，得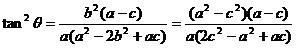=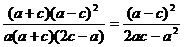，……………12分

若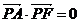，则PA⊥PF，表明△PAF是直角三角形，从而有 ?PA?² +?PF?² =?AF?²，

∴ （x₀ + a）² + y₀² +（x₀－c）² + y₀² =（a + c）²，∴  x₀ ² + y₀² +（a－c）x₀ = ac．……………8分

y₀ =（x₀ + a）tanq =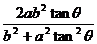．……………………………………………………………………6分

所以，有 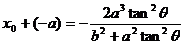，即，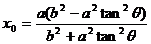

（b² + a² tan²q）x² + 2a³ tan²q ? x + a⁴ tan²q－a²b² = 0．（2）…………………………………………4分

因为点A（－a，0）和P（x₀，y₀）的坐标满足方程（1）和（2），

则直线PA的方程为 y =（x + a）tanq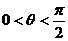，．（1）

将直线PA的方程与椭圆方程联立，消去y后，得

解法二   由题意知A（－a，0），F（c，0），a² = b² + c²，．