
6、 向心加速度:(1)方向:总是指向圆心,时刻发生变化(a是一个变加速度)。(2)大小:a=v2/r=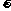 2r=(2
2r=(2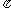 /T)2r=(2
/T)2r=(2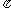 f)2r。(3)物理意义:只描述线速度方向改变的快慢。(4)注意:a与r是成正比还是成反比?若
f)2r。(3)物理意义:只描述线速度方向改变的快慢。(4)注意:a与r是成正比还是成反比?若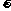 相同,a与r成正比;若v相同,a与r成反比;若是r相同,a与
相同,a与r成正比;若v相同,a与r成反比;若是r相同,a与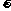 2成正比,与v2成反比。
2成正比,与v2成反比。
5、
V、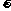 、T、f的关系:T=1/f,f=1/T,
、T、f的关系:T=1/f,f=1/T,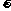 =2
=2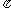 /T=2
/T=2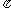 f,v=2
f,v=2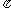 r/T=2
r/T=2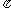 rf,v=r
rf,v=r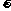 ,
,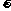 =v/r
=v/r
4、 频率f:质点单位时间内沿圆周绕圆心转动的快慢,国际单位是Hz.
3、 周期T:质点沿圆周运动一周所用的时间,国际单位是s.
2、
角速度:(1)大小: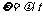 ,国际单位是rad/s。(2)物理意义:描述质点绕圆心转动的快慢。
,国际单位是rad/s。(2)物理意义:描述质点绕圆心转动的快慢。
1、 线速度:(1)方向:就是圆弧该点的切线方向。(2)大小:v=s/t(s是t时间内通过的弧长)。(3)物理意义:描述质点沿圆弧运动的快慢。
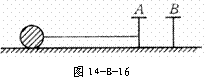
13..如图14-B-16所示,光滑的水平桌面上,钉有两枚铁钉A和B,相距0.1m,长1m的柔软细线,一端拴在A上,另一端拴住一个质量为500g的小球,小球的初始位置在AB连线上A的一侧,把细线拉直,给小球以2m/s,垂直于细线方向的水平速度,使它做圆周运动,使绳子逐渐被缠绕在AB上,已知细线所能承受的最大拉力为8N,问:小球从开始运动到细线断裂用时多少?
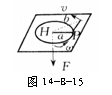
12.如图14-B-15所示,在水平固定的光滑平板上,有一质量为M的质点P,与穿过中央小孔H的轻绳一端连着。平板与小孔是光滑的,用手提着绳子下端,使质点做半径为a,角速度为ω的匀速圆周运动,若绳子迅速放松至某一长度b而拉紧,质点就能在以半径为b的圆周上做匀速圆周运动,求质点由半径a到b所需的时间及质点在半径为b的圆周上运动的角速度。
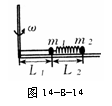
11.如图14-B-14所示,当质量分别为m1和m2的两球以等角速度ω绕轴在光滑平面上旋转时,突然绳烧断L1的瞬时,m1的加速度大小是多少?方向怎样?
10.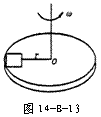 如图14-B-13所示,水平转盘上放有质量为m的物块,当物块到转轴的距离为r时,连接物块和转轴的绳刚好被拉直(绳上张力为零)。物体和转盘间最大静摩擦力是其正压力的μ倍.求:
如图14-B-13所示,水平转盘上放有质量为m的物块,当物块到转轴的距离为r时,连接物块和转轴的绳刚好被拉直(绳上张力为零)。物体和转盘间最大静摩擦力是其正压力的μ倍.求:
(l)当转盘的角速度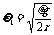 时,细绳的拉力T1=
;
时,细绳的拉力T1=
;
(2)当转盘的角速度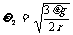 时,细绳的拉力T2=
。
时,细绳的拉力T2=
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com