2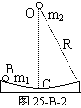．如图25-B-2所示，地面上有一段光滑圆弧槽，其弧长10cm，半径为2m，在圆弧轨道的B点放有一质量为m₁的光滑小球(可视为质点)，在圆弧的圆心处放一静止小球m₂，且m₁≠m₂，现将它们同时无初速释放(C为圆弧的中心)则( 　　)

A．　 m₁先到达C点　

B．　 m₂先到达C点　

C．两者同时到达C点

D．因为它们质量不等，无法判断谁先到达C点

1．两个单摆在做简谐振动，当第一个单摆完成5次全振动时，第二个单摆完成8次全振动，则第一个单摆与第二个单摆长度之比为(　　 )

A．5︰8　　 　　　B．8︰5　　　

C．25︰64　　　　 D．64︰25

12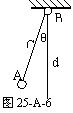．如图25-A-6所示，很长的细线C系着一个小球A做成单摆，在其悬点O处还固定另一细绳d，串在绳子上的小球B能沿绳子下滑，现将A球偏离垂线d一个很小的角度θ，B球停在悬点O处，使它们同时无初速开始运动，假如A和B正好能相碰，求B和绳子之间的摩擦力与B球的重力之比。　

(该题考查了单摆运动的周期性，根据运动的时间相等再利用运动学规律可以求

(该题考查了单摆在整个运动过程中的受力及能量关系，利用机械能守恒和牛顿第二定律即可解决)

11．汽车在一条起伏不平的公路上行驶，路面上凸起处相隔的距离大约都是16m，汽车的车身是装在弹簧上，当汽车以8m/s的速度行驶时，车身起伏得最激烈，则车身与弹簧构成的系统的固有频率是多少？

(该题考查的是受迫振动中的共振条件：即f_驱=f_固)

10．在相同时间内单摆甲做了10次全振动，单摆乙做了6次全振动，两个单摆的摆长差△L=16cm，求摆长L₁和L₂各为多少？

(该题考查对单摆周期公式的灵活运用)

9．振动周期为2秒的单摆叫秒摆，秒摆的摆长为　　 　　，若将此摆移到离地球表面距离等于地球半径的高空，其周期是　　 　秒。

(该题是单摆周期公式的具体应用，结合万有引力定律找出g的相互关系即可求解)

8．一个单摆长为 L ，摆球的质量为m,在最大位移处时，摆线与竖直方向的夹角为α，此时摆球所受的合力为　　　 ，摆球所受的回复力的大小为　　　 ，摆球往复运动时，摆线上最大张力为　　　　　 。

7．一物体在某行星表面受到的万有引力是它在地球表面受到的万有引力的1/4，在地球上走得很准的摆钟搬到此行星上后，此钟的分针走一整圈所经历的时间实际上是　　　 。

(该题考查了不同星体表面的重力加速度对单摆周期的影响，利用万有引力定律求解)

6．如图25-A-5所示，在一根张紧的绳子上挂着4个单摆小球a、b、c、d，它们的摆长分别是L_b=1.0m，L_a=3L_b/4，L_c=L_b/2，L_d=L_b/4，当用0.5H_Z的周期性外力拨动张紧的绳时，稳定后摆球振动的振幅最大的是(　　 )

A．a球　 B．b球　

C．c球　　 D．d球

(受迫振动中如果固有频率不可能等于驱动力的频率，则根据共振曲线可知当它们之间相差越小振幅越大)

5．若单摆的摆长不变，摆球的质量增加为原来的4倍，摆球经过平衡位置的速度减小为原来的1/2，则单摆振动的(　　　 )

A．　 频率不变，振幅不变　　　　

B．频率不变，振幅改变

C．频率改变，振幅改变　　　　

D．频率改变，振幅不变

(单摆的频率决定于摆长，与质量、振幅无关。摆球在平衡位置的速度改变，其振幅相应改变)