
5.不等式有丰富的实际背景,是刻画区域的重要工具。刻画区域是解决线性规划问题的一个基本步骤,教学中可以从实际背景引入二元一次不等式组。
4.一元二次不等式教学中,应注重使学生了解一元二次不等式的实际背景。求解一元二次不等式,首先可求出相应方程的根,然后根据相应函数的图象求出不等式的解;也可以运用代数的方法求解。鼓励学生设计求解一元二次不等式的程序框图。
3.在数列的教学中,应保证基本技能的训练,引导学生通过必要的练习,掌握数列中各量之间的基本关系。但训练要控制难度和复杂程度。
2.等差数列和等比数列有着广泛的应用,教学中应重视通过具体实例(如教育贷款、购房贷款、放射性物质的衰变、人口增长等),使学生理解这两种数列模型的作用,培养学生从实际问题中抽象出数列模型的能力。
1.解三角形的教学要重视正弦定理和余弦定理在探索三角形边角关系中的作用,引导学生认识它们是解决测量问题的一种方法,不必在恒等变形上进行过于繁琐的训练。
3.不等式(约16课时)
(1)不等关系
通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景。
(2)一元二次不等式
①经历从实际情境中抽象出一元二次不等式模型的过程。
②通过函数图象了解一元二次不等式与相应函数、方程的联系。
③会解一元二次不等式,对给定的一元二次不等式,尝试设计求解的程序框图。
(3)二元一次不等式组与简单线性规划问题
①从实际情境中抽象出二元一次不等式组。
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组(参见例2)。
③从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决(参见例3)。
(4)基本不等式: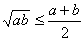
①探索并了解基本不等式的证明过程。
②会用基本不等式解决简单的最大(小)值问题(参见例4)。
说明与建议
2.数列(约12课时)
(1)数列的概念和简单表示法
通过日常生活中的实例,了解数列的概念和几种简单的表示方法(列表、图象、通项公式),了解数列是一种特殊函数。
(2)等差数列、等比数列
①通过实例,理解等差数列、等比数列的概念。
②探索并掌握等差数列、等比数列的通项公式与前n项和的公式。
③能在具体的问题情境中,发现数列的等差关系或等比关系,并能用有关知识解决相应的问题(参见例1)。
④体会等差数列、等比数列与一次函数、指数函数的关系。
1.解三角形(约8课时)
(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
7.在本模块的教学中,应鼓励学生使用计算器和计算机探索和解决问题。例如,求三角函数值,求解测量问题,分析y=Asin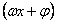 中参数变化对函数的影响等。在三角函数、平面上的向量和三角恒等变换相应的内容中可以插入数学探究或数学建模活动。
中参数变化对函数的影响等。在三角函数、平面上的向量和三角恒等变换相应的内容中可以插入数学探究或数学建模活动。
参考案例
例1 海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。下面是某港口在某季节每天的时间与水深关系表:
|
时刻 |
水深/米 |
时刻 |
水深/米 |
时刻 |
水深/米 |
|
0:00 |
5.0 |
9:00 |
2.5 |
18:00 |
5.0 |
|
3:00 |
7.5 |
12:00 |
5.0 |
21:00 |
2.5 |
|
6:00 |
5.0 |
15:00 |
7.5 |
24:00 |
5.0 |
(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值。
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?
(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
数学5
在本模块中,学生将学习解三角形、数列、不等式。
学生将在已有知识的基础上,通过对任意三角形边角关系的探究,发现并掌握三角形中的边长与角度之间的数量关系,并认识到运用它们可以解决一些与测量和几何计算有关的实际问题。
数列作为一种特殊的函数,是反映自然规律的基本数学模型。在本模块中,学生将通过对日常生活中大量实际问题的分析,建立等差数列和等比数列这两种数列模型,探索并掌握它们的一些基本数量关系,感受这两种数列模型的广泛应用,并利用它们解决一些实际问题。
不等关系与相等关系都是客观事物的基本数量关系,是数学研究的重要内容。建立不等观念、处理不等关系与处理等量问题是同样重要的。在本模块中,学生将通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,理解不等式(组)对于刻画不等关系的意义和价值;掌握求解一元二次不等式的基本方法,并能解决一些实际问题;能用二元一次不等式组表示平面区域,并尝试解决一些简单的二元线性规划问题;认识基本不等式及其简单应用;体会不等式、方程及函数之间的联系。
内容与要求
6.在三角恒等变换的教学中,可以引导学生利用向量的数量积推导出两角差的余弦公式,并由此公式推导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式。鼓励学生独立探索和讨论交流,引导学生推导积化和差、和差化积、半角公式,以此作为三角恒等变换的基本训练。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com