
若点E′在第二象限,∴设E′(-4 , 5
, 5 )且
)且 > 0,
> 0,
∵ 点E′到 轴的距离与到
轴的距离与到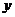 轴的距离比是5∶4 ,
轴的距离比是5∶4 ,
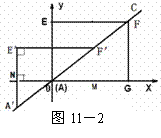
② 如图11-2
∴ 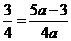 . ∴
. ∴  =
= 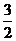 ,E′( 6,
,E′( 6, 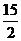 ) .
) .
∴ △ E′A′F′∽△ M A′A ,得 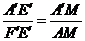 .
.
延长E′A′交 轴于M ,得A′M = 5
轴于M ,得A′M = 5 -3, AM = 4
-3, AM = 4 .
.
∵ ∠E′=∠A′M A = 90°, ∠E′A′F′=∠ M A′A ,
 ∴设E′(4
∴设E′(4 , 5
, 5 )且
)且 > 0 ,
> 0 ,
∵ 点E′到 轴的距离与到
轴的距离与到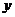 轴的距离比是5∶4 , 若点E′在第一象限 ,
轴的距离比是5∶4 , 若点E′在第一象限 ,
∴ FG =  CD, AG
=
CD, AG
= AD .
AD .
∵ CD = BA = 6, AD = BC = 8 , ∴ FG = 3,AG = 4 . ∴ F(4,3)。
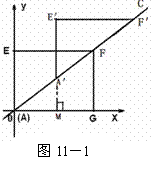
(3)解法一:∵ △A′E′F′是由△AEF沿直线AC平移得到的 ,
∴ E′A′= E A = 3,E′F′= E F = 4 .① 如图11-1
∴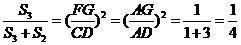 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com