
[佳作示例]
绝望中的希望
高档的裙子被一个小小的烟头烧出了一个窟窿,看着完美作品转眼成空的你如何是好呢?或许你会咒骂那承担了千古罪名的烟头毁了你艺术的高峰,或许你会终日想着如何把它复原到起初无瑕的完美而再无新作诞生……可是他却不一样,谁说这窟窿不是上帝仁慈的扶持?复制几个,饰以金边,一条“金边凤尾裙”把这裁缝推上了更高的云端。世界很多时候就是这样,正如《无望井》一书里让我感触最深的一句话:“在最深的绝望中,你会看到最美丽的希望的星空。”绝望与希望本来就只差一线,可见,绝望往往是希望的开始。
以勇气挣开绝望的束缚,用心去拓展希望的疆域,一个人总能创造出意料之外也是情理之中的奇迹。国民党的第五次围剿终于冲破了我军战士们死守的防线,人民的军队陷入了最大的危机中,这是令人绝望的黑暗。可是深知历史发展的我们都清楚,正是这次危机促成红军壮烈的二万五千里长征。在毛主席的领导下,人民军队在陕甘宁地区凭着地形的优势从此站稳了脚跟。更不用说,后来还在那里团结了西北人民强大的力量,成立了敌后根据地,给予了日本侵略者最沉重的打击,并最终打败国民党反动派,建立了和平自由民主的社会主义新中国。如此看来,这次危机正像那裙子上的窟窿一样,是让红色革命力量化劣势为优势、走出失败的阴影、夺取全国最后胜利的转机。
绝望的危机总能激发人最深最尖锐的智慧,而往往正是逼近中压力下迸发的思考照亮了漆黑一片的夜空。我很佩服中国人民“置诸死地而后生”的见识与睿智,正如金庸小说《天龙八部》中主人公虚竹的那一步棋,失了一大片疆土,几乎陷入毫无希望的陷阱,可与此同时却换得柳暗花明的新局面。人是应该有点放手的胸襟,为什么非要原来裙子的完整呢?为什么非要死守原来的完美呢?完美无缺反而失去了创新的空间,绝望之中正是新希望的孕育源头,敢于尝试创新可能给予你更意想不到的“洞天之所”啊!又想起那孔明闻名于世的“空城计”,原有的势单力薄是绝望,但这智者并没有因此放弃,带着对司马懿的了解与放手一搏的信心,他大开城门,焚香弹琴,以出人意料的计谋赢得了漂亮的胜利。一出绝唱千古的“空城计”,让诸葛亮从绝望的危机中觅得一线生机,而这临危急智的产生,客观地讲若是离开了当时上天无路、入地无门的绝望处境,恐怕是难以想象的。
裙子破了,不灰心,“金边凤尾裙”横空出世;
革命失利,不气馁,全国胜利的曙光照彻神州;
身陷绝境,不放弃,为后人留下千古佳话。
挣开绝望吧,你就能看到希望的新光!
寻找生活的契机
陆游行于山水之间,发出了“山重水复疑无路,柳暗花明又一村”的感慨,在今天的生活中,或许等待我们的是深不可测的悬崖,或许等待我们的铺满荆棘的小路,或许等待我们的是惊涛骇浪的大海,但只要我们懂得寻找生活的契机,希望与目标离我们还远吗?因此,要学会寻找生活的契机。
寻找生活的契机,必须付出努力去应对困难。一个裁缝因吸烟而把高档裙子烧了一个窟窿,为挽回损失,在裙子四围剪了许多窟窿并精心加以修饰,后来这裙子就成了流行一时的款式,生意十分红火。从遭受损失到生意变得红火这过程中,裁缝在自己的努力下寻找到免遭损失的方法,也为自己的成功带来的契机。其实,生活并不缺乏契机,在于你有没有付出努力去寻找。
寻找生活的契机,必须学会转化角度思考生活。相信《泰坦尼克号》这部电影是家喻户晓的,但其背后曾有这么一个真实的故事。一家不富裕的人在省吃俭用后终于储够钱去乘船旅游,但在出发前的一个星期,儿子因被狗咬伤而全家被隔离,以防会有狂犬病的感染。因此,全家错失了旅游的机会。男孩的父亲开始伤心,怨恨儿子的顽皮,但后来得知原来要乘的船沉后,他转悲为喜,拥抱了儿子并感谢了儿子。或许生活中在很多不顺,但每件事都有多面,学会从另一角度思考一顺心的事,或许生活的契机就在你身旁。其实,生活并不缺乏契机,在于你有没有学会转化思考。
寻找生活的契机,必须学会乐观地生活。亘古及今,无数英雄人物的成就在于经历了万难之后才成功的。贝多芬经历了疾病的折磨,仍乐观向上,积极应对生活而创作了《命运交响曲》,流芳百世;作家海伦面对生活的多番变化、残疾的折磨,也仍乐观向上,无数名篇佳作。生活可以是美好的,也可以是万丈深渊,在于你自己怎样看待。其实,生活并不缺乏契机,在于你有没有乐观看待生活。
我们身边的生活或许是阴雨连绵,或许是晴空万里,但不管是怎样的气候,都潜藏着无限的生活契机。努力面对,转化思维,积极乐观地生活吧,我们就会像裁缝一样,让成功的契机始终充满我们的生活。
意外与困难的门扉之后
当你不小心走上了计划外的道路,请相信“条条大路通罗马”的古语,满怀信心地往前走吧。
当被意外的风吹离了计划的航线,请看到陌生却又光亮的灯塔,清醒勇敢地掌好舵吧。
当被错误的地图带进了死胡同,请思考忽略的可能性吧,冷静沉着地越过阻碍。
因为,意外并不可怕,可怕的是向意外与困境投降。一位裁缝将高档裙子上烧出来的窟窿装饰一番,成为时髦的“金边凤尾裙”。你看,像这样的事情是存在的。我们从来不必向意外与困难投降,只要我们愿意挑战。
以一颗信心,迎着未知的意外与困难前进。麦哲伦完成环球航行,当中的惊险可想而知,然而在遇到困难及海上疾病时,他并没有放弃,甚至当机立断地改航道,意外地发现许多海峡海岛。画错的细节往往让画家们无所适从,然而妙手一挥,也可促成点睛之笔。关键是信心,信自己,也信生活,信这个机遇遍布的世界。
以一双亮眼,察觉意外与困难中潜藏的奇迹。炼丹师们造成的爆炸本是意外本是失败,却有人从中看到了可能,进而发明了火药。商机也是这样,善于观察,善于了解细节的眼盯上的,像刚开始不被看好的高科技产业、电脑市场,却能被有识之士看上。关键是敏锐的眼光,看细节,看世界,看这个广阔的未来。
以一身智慧,思索意外中埋藏着的道理与意义。尽管灵感是促成意外向成功转化的总是要因素,但更多时候,灵机一触不及深思熟虑可靠。从“推”与“敲”的思考中,我们了解到意外而来的难题,就像诗歌中的炼字,需要去想而不是横冲直撞。百事可乐公司总裁也曾陷入要将公司卖给可口可乐集团的困境,然而苦心经营几载,,终于还是用思想,用智慧垒起了公司的基业。关键是智慧的头脑,想问题,想方法,想这个世界的法则。
生活本身就是意外的。有人去算一个人诞生于世的几率,分母已经可以用无限大去形容了。生活不可能摆脱意外。既然我们意外降生,从而活了下来,困境与意外,又有什么可怕的呢?
走吧。当生活向你开了一扇意外的,甚至是不好的门,面对艰难的前路,像裁缝那样走下去,也总是有未来的。
门扉之后,将是一个新世界。
[扣材分析示例]
然而,面对空前的灾难,灾区人民没有陷入悲观的绝望之中,而是勇敢地从废墟中爬出来,从失去亲人的悲痛中挺过来,擦干眼泪,重建家园。我们坚信,在强劲有力充满人文关怀的党中央的英明领导下,在全中国人民的大力支持下,我们同在一起,我们共克难关。我们坚信,众志成城,天佑中华。我们坚信,汶川的明天会更好!
●农业及其分类
●农业的地区分布:
①东、西部差异: 400毫米等降水量线
例题1.
(1)农业分布:大致以_________毫米等降水量线为界,把我国分为东部农耕区和西部牧业区。
(2)东部:种植业、林业、渔业主要分布在我国东部。其中平原地区以________业为主;林业集中在_________和_______的天然林区及_________的人工林区;沿海地区是海洋捕捞和海水养殖基地;_________________地区是我国淡水渔业最发达的地区。
(3)西部:天然草场广布,以___________业为主,分布有四大牧区:_____________、_____________、____________、_____________。种植业只分布在有灌溉水源的平原、河谷和绿洲地区。
②南、北方种植业的差异:
例题2.
|
|
耕地类型 |
作物熟制 |
主要农作物 |
|
北方地区 |
|
|
|
|
南方地区 |
|
|
|
③三大棉区
例题3.下列不属于我国的三大棉区之一的是 ( )
A.黄河流域 B.长江流域 C.新疆南部 D.东北平原
④主要商品粮基地
例题4.图中我国的九大商品粮基地
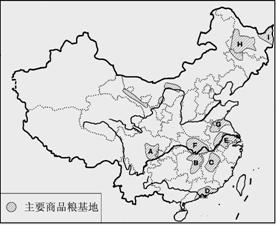
AA_____________B_____________C_____________
D_____________E_____________F_____________
G_____________H_____________I_____________
● 因地制宜发展农业
因地制宜发展农业:①东部沿海发达地区要积极发展________农业,(从交通、地形、气候、社会经济条件分析有利条件)②中部地区建立高产高效的__________基地;③西部地区坚决实行__________,大力发展_____________农业、___________农业。
32、我国的工业
●工业生产 及其特点
●工业分布特点:(沿海)、(沿河)、( 沿交通线) 工业的空间分布
例题1.
(1)沿海:.沿海地区(长江三角洲、辽中南、京津唐、珠江三角洲)是工业最发达的经济核心区。
(2)沿河:_________沿江经济发达地带;_________流域是能源开发的重要工业带;
(3)沿交通线:京广、京沪、哈大等铁路沿线形成许多工业基地;
例题2.
(1).下列城市中,完全属于沪宁杭工业区的是 ( )
A.上海、深圳、沈阳 B.北京、天津、苏州
C天津、无锡、广州 D.苏州、无锡、常州
(2).辽中南工业区的特点是 ( )
A.以重工业为主 B.以轻工业为主
C.以能源工业为主 D.以高新技术产业为
例题3.
(1) 图中所示为我国的___________工业基地,它是我国的_________
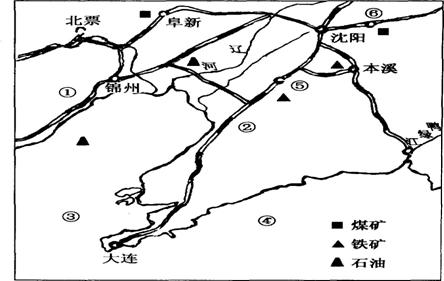
A. 我国最大的综合性工业基地
B. 我国北方著名的重工业基地
C. 我国北方最大的综合性工业基地
D. 以轻工业为主的综合性工业基地
(2)如图:①是__________________铁路,②______________铁路
(3)③_____________海④________________海
(4)⑤号称我国的钢都,它是____________________⑥是工业城市____________________
● 发展高新技术产业: 例题4.
(1)特征:1.从业人员中_________所占的比重大;2.销售收入中用与______________的费用比例大;3.产品更新换代_______。
(2)分布特点:高新技术产业开发区多依附于大城市,呈点状分布。北京____________是我国第一个国家级高新技术产业开发区。
(3) 开发侧重点:沿海地区以智力资源和技术力量为依托,侧重科技园区型高新技术产业; 沿边地区发展以(贸易导向型)的产业;内地多发展与(军工有密切关系)的产业。
例题5.下列关于高新技术产业的叙述正确的是 ( )
A.高新技术产业布局在技术发达、知识密集、人才聚集的地域
B.中国高新技术产业起步早,但发展缓慢
C.高新技术产业开发区倾向于依附大城市,呈带状分布
D.北京、深圳已成为我国高新技术产业的核心。
●交通运输:五种交通运输方式特点的比较 交通运输方式的选择
例题1. 两箱急救药品,从北京运往拉萨,最合适的运输方式是 ( )
A.铁路运输 B.航空运输
C.公路运输 D.水路运输
●目前分布特点:东部密集,西部稀疏。
主要铁路干线
例题2.我国交通运输网络的大致分布格局:东______西_______。(填密或疏)
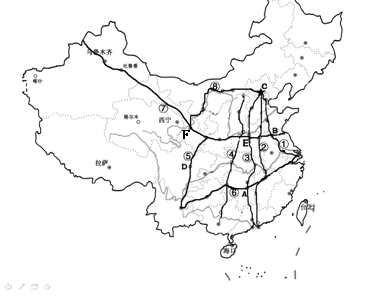
图中所示我国的主要铁路干线
(1)五纵:①______________②________________③________________
④_______________⑤_______________
三横:⑥_________________⑦___________________⑧_____________________
(2)图中铁路枢纽:A______________B_____________C_____________
D_________________E________________
(3)在图中补充青藏铁路、京哈线。
例6某市有小灵通与全球通两种手机,小灵通手机的月租费为25元,接听电话不收费,打出电话一次在3 min以内收费0 2元,超过3 min的部分为每分钟收费0
2元,超过3 min的部分为每分钟收费0 1元,不足1 min按1
min计算(以下同)
1元,不足1 min按1
min计算(以下同) 全球通手机月租费为10元,接听与打出的费用都是每分钟0
全球通手机月租费为10元,接听与打出的费用都是每分钟0 2元
2元 若某人打出与接听次数一样多,每次接听与打出的时间在1 min以内、1到2
min以内、2到3 min以内、3到4 min以内的次数之比为4∶3∶1∶1
若某人打出与接听次数一样多,每次接听与打出的时间在1 min以内、1到2
min以内、2到3 min以内、3到4 min以内的次数之比为4∶3∶1∶1 问,根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1 min)
问,根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1 min)
解:设小灵通每月的费用为y1元,全球通的费用为y2元,分别在1 min以内、2 min以内、3 min以内、4 min以内的通话次数为4x、3x、x、x,则
y1=25+(4x+3x+x+x)×0 2+0
2+0 1x=25+1
1x=25+1 9x,
9x,
y2=10+2(0 2×4x+0
2×4x+0 4×3x+0
4×3x+0 6x+0
6x+0 8x)=10+6
8x)=10+6 8x
8x
令y1≥y2,即25+1 9x≥10+6
9x≥10+6 8x,
8x,
解得x≤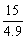 ≈3
≈3 06
06
∴总次数为(4+3+1+1)×2×3 06=55
06=55 1
1
故当他每月的通话次数小于等于55次时,应选择全球通,大于55次时应选择小灵通
例7 某市收水费的方法是:水费=基本费+超额费+耗损费,若每月用水量不超过最低限量am3时,只付基本费8元及每户每月的定额耗损费c元,若用水量超过am3时,除了付同上的基本费和耗损费之外,超过部分每m3付b元的超额费,已知耗损费不超过5元
该市一家庭今年一月、二月、三月份的用水量和支付费用如下表所示:
|
月份 |
用水量 |
水费 |
|
一月 |
9m3 |
9元 |
|
二月 |
15m3 |
19元 |
|
三月 |
22m3 |
33元 |
根据上面表格中的数据求a,b,c
解:设每月用水量为xm3,支付费用为y元,由收费方法知:
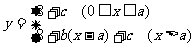
依题意:0<c£5,∴ 8+c£13
所以该用户第二、三月份的用水量均大于am3,
将x=15,x=22代入上面的第二个式子,得:
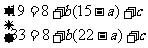 ,∴ b=2,2a=c+19
,∴ b=2,2a=c+19
若该用户一月份的用水量大于am3,
则9=8+2(9-a)+c,2a=c+17与2a=c+19矛盾,
∴ a³9
将y=9代入y=8+c得c=1,
∴ a=10, b=2, c=1
例8已知扇形的周长为10,求扇形半径r与面积S的函数关系式及此函数的定义域、值域
解:设扇形的弧长为l,则l=10-2r,
∴S=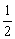 lr=(5-r)r=-r2+5r
lr=(5-r)r=-r2+5r
由 得
得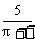 <r<5
<r<5
∴S=-r2+5r的定义域为(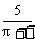 ,5)
,5)
又S=-r2+5r=-(r-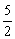 )2+
)2+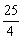 且
且
r=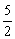 ∈(
∈(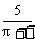 ,π),
,π),
∴当r=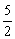 时,S最大=
时,S最大=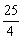

又S>-52+5×5=0,
∴S=-r2+5r,r∈(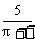 ,5)的值域为(0,
,5)的值域为(0,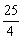 ]
]
小结:
1 求函数的解析式主要有待定系数法和换元法
求函数的解析式主要有待定系数法和换元法 如果已知函数解析式的构造时,可以用待定系数法求,如函数为二次函数,可设为y=ax2+bx+c(a≠0)
如果已知函数解析式的构造时,可以用待定系数法求,如函数为二次函数,可设为y=ax2+bx+c(a≠0)
2 根据实际问题求函数表达式,是应用函数知识解决实际问题的基础,在设定或选定变量去寻求等量关系并求得函数表达式后,还要注意函数定义域常受到实际问题本身的限制
根据实际问题求函数表达式,是应用函数知识解决实际问题的基础,在设定或选定变量去寻求等量关系并求得函数表达式后,还要注意函数定义域常受到实际问题本身的限制
学生练习
题组一:
1 若f(sinx)=2-cos2x,则f(cosx)等于
若f(sinx)=2-cos2x,则f(cosx)等于
A 2-sin2x B
2-sin2x B 2+sin2x C
2+sin2x C 2-cos2x D
2-cos2x D 2+cos2x
2+cos2x
解析:∵f(sinx)=2-(1-2sin2x)=1+2sin2x,
∴f(cosx)=f(sin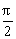 -x)=1+2sin2(
-x)=1+2sin2(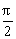 -x)=1+2cos2x=2+cos2x
-x)=1+2cos2x=2+cos2x
答案:D
2 已知f(
已知f(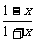 )=
)=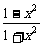 ,则f(x)的解析式可取为
,则f(x)的解析式可取为
A
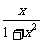 B
B -
-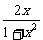 C
C
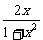 D
D -
-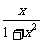
解析:令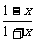 =t,则x=
=t,则x=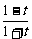 ,
,
∴f(t)=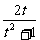
 ∴f(x)=
∴f(x)=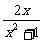

答案:C
3 函数f(x)=|x-1|的图象是
函数f(x)=|x-1|的图象是
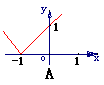
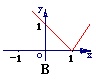
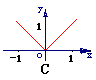
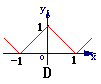
解析:转化为分段函数y=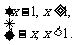
答案:B
4 函数y=
函数y=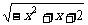 的定义域为______,值域为______
的定义域为______,值域为______
答案:[-1,2]
,[0,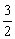 ]
]
5 函数y=
函数y=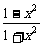 的值域是
的值域是
A [-1,1] B
[-1,1] B (-1,1] C
(-1,1] C [-1,1) D
[-1,1) D (-1,1)
(-1,1)
解法一:y=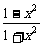 =
=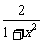 -1
-1
∵1+x2≥1,
∴0<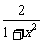 ≤2
≤2 ∴-1<y≤1
∴-1<y≤1
解法二:由y=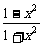 ,得x2=
,得x2=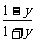

∵x2≥0,∴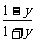 ≥0,解得-1<y≤1
≥0,解得-1<y≤1
解法三:令x=tanθ(-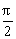 <θ<
<θ<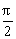 ),
),
则y=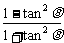 =cos2θ
=cos2θ
 ∵-π<2θ<π,
∵-π<2θ<π,
∴-1<cos2θ≤1,即-1<y≤1
答案:B
6 如果f[f(x)]=2x-1,则一次函数f(x)=___________
如果f[f(x)]=2x-1,则一次函数f(x)=___________
解析:设f(x)=kx+b,则f[f(x)]=kf(x)+b=k(kx+b)+b=k2x+kb+b
由于该函数与y=2x-1是同一个函数,
∴k2=2且kb+b=-1 ∴k=±
∴k=±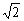

当k=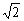 时,b=1-
时,b=1-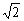 ;
;
当k=-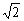 时,b=1+
时,b=1+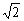

答案:f(x)=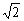 x+1-
x+1-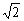 或f(x)=-
或f(x)=-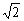 x+1+
x+1+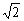
7 已知f(x2-4)=lg
已知f(x2-4)=lg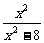 ,则f(x)的定义域为__________
,则f(x)的定义域为__________
解析:设x2-4=t,则t≥-4,x2=4+t
∴f(t)=lg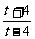
 ∴f(x)=lg
∴f(x)=lg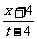 (x≥-4)
(x≥-4)
由 得x>4
得x>4
答案:(4,+∞)
8 用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域
用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域
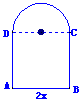 解:∵AB=2x,则
解:∵AB=2x,则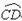 =πx,AD=
=πx,AD=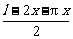

∴y=2x·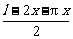 +
+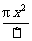 =-(
=-(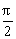 +2)x2+lx
+2)x2+lx
由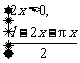 >0,解得0<x<
>0,解得0<x<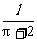

9 已知函数f(x)=
已知函数f(x)=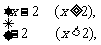 则f(lg30-lg3)=________;不等式xf(x-1)<10的解集是___________
则f(lg30-lg3)=________;不等式xf(x-1)<10的解集是___________
解析:f(lg30-lg3)=f(lg10)=f(1)=-2,
f(x-1)=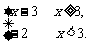
当x≥3时,x(x-3)<10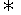 -2<x<5,故3≤x<5
-2<x<5,故3≤x<5
当x<3时,-2x<10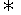 x>-5,故-5<x<3
x>-5,故-5<x<3
总之x∈(-5,5)
答案:-2 {x|-5<x<5}
10 定义“符号函数”f(x)=sgnx=
定义“符号函数”f(x)=sgnx=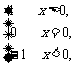
则不等式x+2>(x-2)sgnx的解集是___________
解析:分类讨论
答案:(-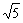 ,+∞)
,+∞)
题组二:
1 设f(2x+1)=x,f-1(x)是f(x)的反函数,则f-1(2)=
设f(2x+1)=x,f-1(x)是f(x)的反函数,则f-1(2)= 
2 已知函数f(x)=
已知函数f(x)=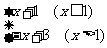 ,则f[f(5/2)]=
,则f[f(5/2)]= 
3 在一定范围内,某种产品的购买量y吨与单价x元之间满足一次函数关系,如果购买1000吨,每吨价格为800元,购买2000吨,每吨为700元,一客户购买400吨,单价应该是( )
在一定范围内,某种产品的购买量y吨与单价x元之间满足一次函数关系,如果购买1000吨,每吨价格为800元,购买2000吨,每吨为700元,一客户购买400吨,单价应该是( )
A 820元 B
820元 B 840元 C
840元 C 860元 D
860元 D 880元
880元
4 若函数y=f(x)存在反函数,则方程f(x)=c(c为常数)
若函数y=f(x)存在反函数,则方程f(x)=c(c为常数)
A 有且只有一个实根 B
有且只有一个实根 B 至少有一个实根
至少有一个实根
C 至多只有一个实根 D
至多只有一个实根 D 没有实数根
没有实数根
5 已知f(x-1/x)=x2+1/x2,则f(x)=
已知f(x-1/x)=x2+1/x2,则f(x)=
6 函数f(x)是一个偶函数,g(x)是一个奇函数,且f(x)+g(x)=1/(x-1),则f(x)=
函数f(x)是一个偶函数,g(x)是一个奇函数,且f(x)+g(x)=1/(x-1),则f(x)= 
7 设函数f(x)=f(1/x)lgx+1,则f(10)的值是
设函数f(x)=f(1/x)lgx+1,则f(10)的值是
8 已知f(x)=log2(x+1),当且仅当点(x,y)在y=f(x)的图象上运动时,点(x/2,y/3)在y=g(x)的图象上运动,求y=g(x)的解析式
已知f(x)=log2(x+1),当且仅当点(x,y)在y=f(x)的图象上运动时,点(x/2,y/3)在y=g(x)的图象上运动,求y=g(x)的解析式
9 若函数f(x)=(ax+b)/(cx+d)与g(x)=(4x+3)/(2-x)的图象关于直线y=x对称,则a:b:c:d=
若函数f(x)=(ax+b)/(cx+d)与g(x)=(4x+3)/(2-x)的图象关于直线y=x对称,则a:b:c:d=

10 从盛满20升纯酒精的容器里倒出1升,然后用水填满,摇匀后再倒出一升,再用水填满,这样继续进行,如果倒k次(k³1)后共倒出纯酒精x升,倒第k+1次后共倒出纯酒精f(x)升,则函数f(x)的表达式为
从盛满20升纯酒精的容器里倒出1升,然后用水填满,摇匀后再倒出一升,再用水填满,这样继续进行,如果倒k次(k³1)后共倒出纯酒精x升,倒第k+1次后共倒出纯酒精f(x)升,则函数f(x)的表达式为 
4. 已知函数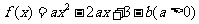 在
在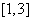 有最大值
有最大值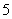 和最小值
和最小值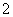 ,求
,求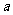 、
、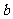 的值.
的值.
3. 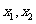 是关于
是关于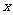 的一元二次方程
的一元二次方程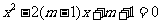 的两个实根,又
的两个实根,又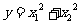 ,
,
求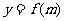 的解析式及此函数的定义域.
的解析式及此函数的定义域.
2. 求函数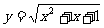 的值域.
的值域.
1. 求函数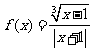 的定义域.
的定义域.
5. 函数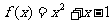 的最小值是_________________.
的最小值是_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com