
1.“重农抑商”是我国封建社会所推行的一项传统政策。该政策首先实行的时期是(
A、春秋 B、战国 C、唐朝 D、明朝
借助复平面上的两点间的距离公式和直线、圆、圆锥曲线等,再利用复数的意义求解问题,比单纯利用代数计算优越的多。
例12.如果复数z满足︱z+i︱+︱z-i︱=2,那么︱z+i+1︱的最小值是( )
A.1 B.
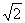 C.2 D.
C.2 D.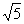
解析:复平面内满足︱z+i︱+︱z-i︱=2的点z的轨迹是线段AB,而︱z+i+1︱表示点Z到P(-1,-1)的距离如图示,
由图知︱z+i+1︱的最小值是1,选A.
以上十种工具是数形结合中常用的模型,熟练掌握这十种模型及相关知识,可以提高同学们数形结合的能力,。
利用向量可以解决线段相等,直线垂直,立体几何中空间角(异面直线的角、线面角、二面角)和空间距离(点线距、线线距、线面距、面面距),建立坐标系,写出坐标,可以“以数定形”。
例10.如图所示,P是正方形的ABCD的对角线BD上一点,四边形PECF是矩形,
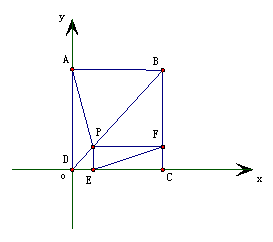 求证:(1).PA=EF
求证:(1).PA=EF
(2).PA⊥EF
建立如图的坐标系,设正方形的边长是1,︱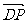 ︱=
︱= ,
,
则A(0,1),P(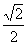
 ,
,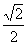
 ),E(
),E(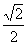
 ,0),F(1,
,0),F(1, 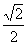
 )
)
∴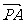 =(-
=(-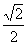
 ,1-
,1-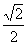
 )
) 
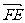 =(
=(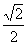
 -1,-
-1,- 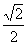
 )
)
(1).∵︱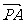 ︱=(-
︱=(-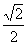
 )
) +(1-
+(1-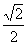
 )
)
=
 -
-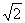
 +1
+1
︱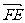 ︱=(
︱=(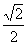
 -1)
-1) + (-
+ (-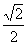
 )
)
=
 -
-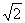
 +1
+1
∴︱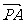 ︱=︱
︱=︱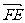 ︱,即PA=EF
︱,即PA=EF
(2). 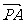 ﹡
﹡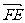 =(-
=(-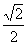
 )(
)(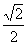
 -1)+(1-
-1)+(1-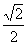
 )(-
)(-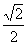
 )
)
=-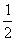

 -
-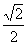
 +
+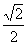
 +
+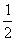

 =0
=0
∴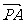 ⊥
⊥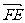 ,即PA⊥EF
,即PA⊥EF
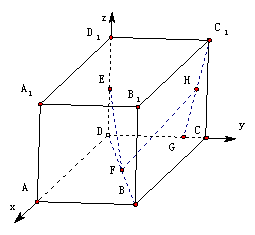 例11.如图所示,在棱长为1的正方形ABCD-A
例11.如图所示,在棱长为1的正方形ABCD-A B
B C
C D
D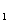 中,E,F分别是DD
中,E,F分别是DD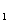 ,BD的中点,G在棱CD上,且CG=
,BD的中点,G在棱CD上,且CG=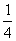 CD,H是C
CD,H是C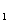 G的中点,
G的中点,
⑴.求证:EF⊥B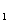 C
C
⑵.求证:EF与C 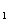 G所成角的余弦值
G所成角的余弦值
⑶.求FH的长
解:如图所示,建立空间直角坐标系D-xyz,
E(0,0, 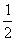 ) F(
) F(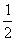 ,
,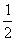 ,0) C(0,1,0) D(0,1,1)
,0) C(0,1,0) D(0,1,1)
B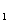 (1,1,1)
G(0,
(1,1,1)
G(0, 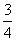 ,0)
,0)
(1).证明: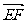 =(
=(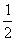 ,
,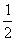 ,-
,-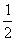 )
) 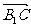 =(-1,0,-1)
=(-1,0,-1)
∵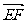 ·
·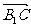 =
=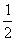 ·(-1)+
·(-1)+ 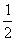 ·0+
·0+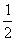 ·(-1)=0
·(-1)=0
∴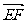 ⊥
⊥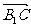 ∴EF⊥B
∴EF⊥B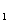 C
C
(2). 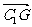 =(0,-
=(0,- 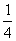 ,-1)
,-1)
∴∣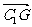 ∣=
∣=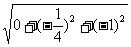 =
=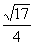
由(1)得
∣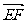 ∣=
∣=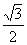
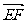 ·
·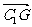 =
=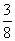 ∴cos
∴cos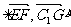 =
=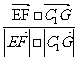 =
=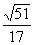
(3). ∵H是C 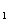 G的中点
G的中点
∴H(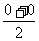 ,
,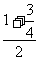 ,
,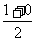 )即H(0,
)即H(0,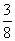 ,
,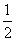 )
)
又∵F(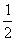 ,
,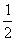 ,0)
,0)
∴FH=︱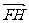 ︱=
︱=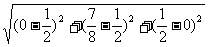 =
=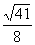
点评:利用空间向量解决立体几何问题,将抽象的逻辑论证转化为代数计算,以数助形,大大降低了空间想象能力,是数形结合的深化。
例9.求sin 20
20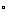 +cos
+cos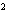 50
50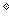 +sin20
+sin20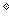 cos50
cos50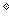 的值。
的值。
解:原式=sin 20
20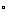 +sin
+sin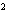 40
40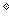 + sin20
+ sin20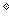 sin40
sin40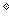
=
sin 20
20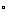 +sin
+sin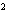 40
40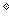 -2 sin20
-2 sin20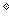 sin40
sin40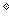 cos120
cos120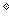
设三角形的外接圆半径是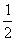 ,三角形的三边分别是a,b,c,则c= sin20
,三角形的三边分别是a,b,c,则c= sin20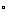 ,b= sin40
,b= sin40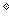
由余弦定理,原式=a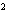 =(2·
=(2·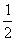 ·sin120
·sin120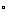 )
) =
=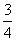
例7.已知a>0且a≠1,试求使方程log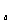 (x-ak)=log
(x-ak)=log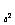 (x
(x -a
-a )
)
有解的实数k的取值范围。
解:原方程等价于0<x-ak=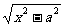
构造曲线C:y= ,直线L:y= x-ak
,直线L:y= x-ak
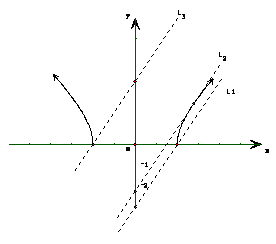 从而使问题转化为直线L和双曲线C:x
从而使问题转化为直线L和双曲线C:x -y
-y =a
=a (y≥0)x轴上半部分有交点,求实数k的取值范围,如图所示:
(y≥0)x轴上半部分有交点,求实数k的取值范围,如图所示:
有三条临界直线L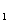 、L
、L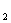 、L
、L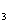
①
当L在L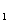 和L
和L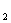 之间时,直线L在y轴上的截距
之间时,直线L在y轴上的截距
② -ak满足-a<-ak<0时L与C有一个交点,
解之可得0<k<1
③ 当L在L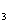 上方时,直线L在y轴上的截距-ak满
上方时,直线L在y轴上的截距-ak满
足a<-ak时L与C有一个交点,
解之可得k<-1
综合①②可得,所求k的取值范围是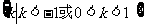
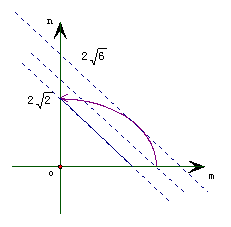 例8.求函数y=
例8.求函数y=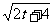 +
+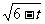 的值域。
的值域。
解:设m=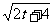 , n=
, n=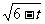 , 则m
, 则m +n
+n =16 (0≤m≤4,0≤n≤2
=16 (0≤m≤4,0≤n≤2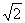 )
)
原函数可变形为y=m+n, y表示直线在n轴上的截距,结合图形可知
y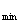 =2
=2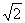 , y
, y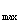 =2
=2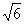
点评:这两道题目可以建立目标函数,然后利用求函数最值的方法解决,但利用圆锥曲线定义数形结合求解,事半功倍,迅速而准确。
例6.已知sin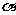 +sin
+sin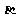 =
=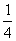 , cos
, cos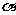 +cos
+cos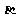 =
=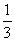 , 求tan(
, 求tan(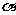 +
+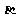 )的值
)的值
 解:点A(cos
解:点A(cos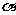 ,sin
,sin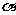 )B(cos
)B(cos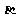 ,sin
,sin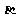 )
)
都在单位圆上,由已知可知A和B的中点C坐标
(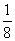 ,
,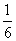 ),则直线AB过定点C
),则直线AB过定点C
∠xOC= 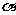 +
+ =
=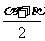
∴tan∠xOC= tan 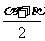 =
=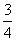
∴tan(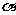 +
+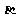 )=
)=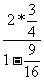 =
=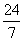
点评:另外,单位圆中的三角函数线可以辅助解决三角不等式(组)问题。
求含有两个变量的线性式子的最值,可以构造直线方程,利用截距的意义解决问题。这一应用在线性规划中体现的很充分---求线性目标函数的最值。
例5.已知x,y满足条件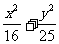 =1,求y-3x的最小值和最大值
=1,求y-3x的最小值和最大值
解:令y-3x=b, 即y=3x+b
由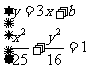 联立可得: 169
联立可得: 169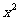 +966y
+966y +16b
+16b -400=0,令⊿≥0得:
-400=0,令⊿≥0得:
-13≤b≤13
∴y-3x的最小值和最大值分别是-13和13。
 求通过变形可以出现
求通过变形可以出现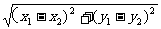 的模式的式子的最值问题,可以优先考虑两点间的距离公式的利用
的模式的式子的最值问题,可以优先考虑两点间的距离公式的利用
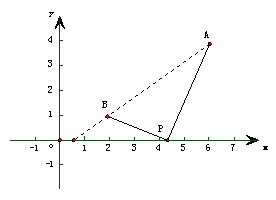
例4.函数y=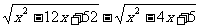 的最小值为
。
的最小值为
。
解析:函数可化为y=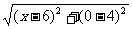 -
-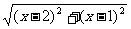
这个式子表示P(x,0)到点A(6,4)和点B(2,1)的差,
由右图可知,当P、A、B三点共线时,
︱PA︱-︱PB︱≤︱AB︱, ︱AB︱=5
函数取得最大值为5
提示:a +b
+b =(
=(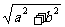 )
) =(
=(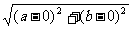 )
) ,表示点(a,b)到原点的距离。
,表示点(a,b)到原点的距离。
分式型的最值问题可以通过变形,利用斜率公式解决。
例3.函数y= 最大值是
,最小值是
。
最大值是
,最小值是
。
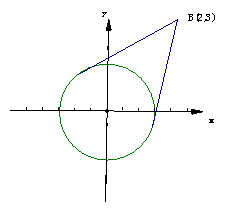 解:函数解析式表示经过A(-cosx,sinx)和B(2,3)两点连线的斜率k,A在单位圆x
解:函数解析式表示经过A(-cosx,sinx)和B(2,3)两点连线的斜率k,A在单位圆x +y
+y =1上,经过A和B两点的直线方程为y-3=k(x-2)
=1上,经过A和B两点的直线方程为y-3=k(x-2)
即kx-y+3-2k=0,由直线和圆的位置关系得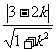 ≤1解之可得;
≤1解之可得; 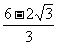 ≤k≤
≤k≤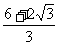
所以函数得最大值是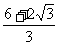 最小值是
最小值是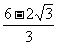 。
。
例1.(1)(2003上海春,5)已知集合A={x||x|≤2,x∈R},B={x|x≥a},且A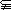 B,则实数a的取值范围是_____.
B,则实数a的取值范围是_____.
解析:(1)a≤-2;
 ∵A={x|-2≤x≤2},B={x|x≥a},又A
∵A={x|-2≤x≤2},B={x|x≥a},又A B,利用数轴上覆盖关系,
B,利用数轴上覆盖关系,
因此有a≤-2.
点评:利用韦恩图和数轴可以直观地解决集合问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com