1．整体把握，理清思路

A.速读课文

a.画出文中结论性的语句;

b.理出文章结构并用简洁的语言概括段意;

B.学生相互交流各自对文章结构和段意的理解,请一位同学回答;

C.教师板书并明确。

整理成书的过程(1)

写作经过 提前发表的原因(2)

(1-3) 内容过简的原因(3)

物种由演变而来(4)

基本观点 介绍研究的方法(5)

(4-7) 家养变异的作用(6)

强调观点的正确(7)

(解说：通过速读，整体感知文章并初步筛选出文章的关键句及主要观点；通过讨论交流，理清文章结构。整体把握全文；通过简洁的段意概括，意在培养学生提炼观点、准确表达的语用能力。)

3．介绍达尔文及其进化论。

请一位学生读浅释1，教师补充。

投影

查理·罗伯特·达尔文(Charles Robert Darmin,1809-1882).英国博物学家,进化论的奠基人.22岁从剑桥大学毕业后,以博物学家的身份乘海军勘探船“贝格尔号”作历时五年的环球旅行，观察并搜集了动植物和地质等 方面的大量材料，经归纳整理与综合分析，形成了生物进化的概念，于1859年出版了震动当时学术界的《物种起源》一书，成为生物学史上的一个转折点。随后骏马征服 《动物和植物在家养下的变异》、《人类起源及性的选择》等书，进一步充实了进化学说的内容。

摘自《辞海》(1999年版)

投影：

进化论 亦称“演化论”，旧译“天演论”。通常指生物办的进货理论。生物进化论是研究生物进化、生物发展规律以及如何运用这些规律的科学，是生物学的一个重要部门。进化论一词最初是拉马克提出。达尔文的《物种起源》一书奠定了进化论的科学基础。而现代生物学的发展，促进了生命起源、物种分化和形成等进化理论的进一步发展，认为生物最初从非生物而来，现代地球上生存的各种生物，有共同的祖先，它们在进化过程中，通过变异、遗传和自然选择，由低级到高级，从简单到复杂，种类由少到多。恩格斯认为达尔文的进化理论是19世纪自然得科学三大发现(能量守恒和转换定律、细胞学说和进化论)之一。

摘自《辞海》(1999年版)

2．关于“导言”。导言即绪论。书的前面有一篇导言，目的是让读者了解全书的要旨，引导读者更好地理解全书的内容。

1．板书课题

投影

辨析下列句子标点使用正确与否。

(1)我们学习《物种起源＊导言》。

(2)我们学习《物种起源》导言。

(3)我们学习《＜物种起源＞序言。

(4)我们学习《物种起源导言》。

投影

达尔文头像

大家一定还记得恩格斯《在马克思墓前的讲话》一文中，把达尔文发现有机界的发展规律和马克思发现人类历史的发展规律相提并论。一百多年前，达尔文的思想改变了人们对世界的看法，一百多年来，这思想影响了一代又一代的人。作为跨世纪的新一代，你了解达尔文吗？你知道进化论吗？今天我们就一起来打开达尔文进化论之门。

10.某人乘坐出租车从A地到乙地，有两种方案：第一种方案，乘起步价为10元，每km价1.2元的出租车；第二种方案，乘起步价为8元，每km价1.4元的出租车，按出租车管理条例，在起步价内，不同型号的出租车行驶的里路是相等的，则此人从A地到B地选择哪一种方案比较适合？

解：设A地到B地距离为mkm，起步价内行驶的路为akm

显然，当m≤a时，选起步价为8元的出租车比较合适

当m>a时，设m=a+x(x>0)，乘坐起步价为10元的出租车费用为P(x)元，乘坐起步价为8元的出租车费用为Q(x)元，则P(x)=10+1.2x，Q(x)=8+1.4x

∵ P(x)-Q(x)=2-0.2x=0.2(10-x)

∴ 当x>10时，P(x)<Q(x)，此时起步价为10元的出租车比较合适

当x<10时，P(x)>Q(x)，此时选起步价为8元的出租车比较合适

当x=10时，P(x)=Q(x)，此时两种出租车任选

[探索题]设关于x的方程2x²－ax－2=0的两根为α、β(α＜β)，函数．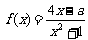

(Ⅰ)求f (α)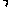f (β)的值；

(Ⅱ)证明f (x)是[α，β]上的增函数；

(Ⅲ)当a为何值时，f (x)在区间[α，β]上的最大值与最小值之差最小？

解：(Ⅰ)由题意知α+β＝，α·β＝－1，∴α²+β²＝，

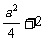f (α)·f (β)＝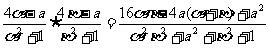

．

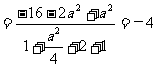(Ⅱ)证明：设α≤x₁<x₂≤β,

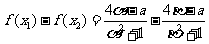
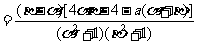
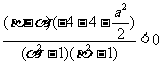
所以f(x)在[α,β]在是增函数.

(法2:导数法)

(Ⅲ)f (x)在区间[α，β]上的最大值f (β)＞0，最小值f (α)＜0，

又∵| f (α)·f (β) |＝4，

∴f (β)－f (α)＝| f (β)|+| f (α)|≥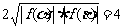

当且仅当| f (β)|＝| f (α)|＝2时取“＝”号，此时f (β)＝2，f (α)＝－2

∴

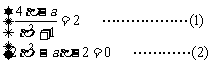
由(1)、(2)得 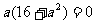，∴a＝0为所求。

9.用一块矩形木板紧贴一墙角围成一直三棱柱空间堆放谷物，已知木板的长为a，宽为b，墙角的两堵墙面和地面两两互相垂直,怎样围法，使直三棱柱的空间最大？这个最大值是多少？

解：如图：A-CC₁---B是二墙面所成直二面角, CC₁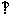面ABC

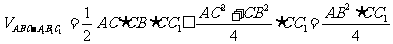(AC=CB时取”=”)

当AB=a,AA₁=b时，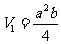

当AB=b,AA₁=a时，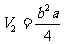

8. (2004全国IV)已知数列{a_n}的前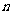项和S_n满足.

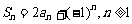(1)写出数列{a_n}的前三项；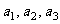

(2)求数列{a_n}的通项公式；

(3)证明：对任意的整数m>4，有

　.

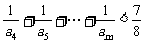(Ⅰ)解：由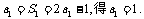

由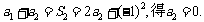

由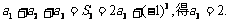

(Ⅱ)解：当时，有

　 ……

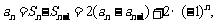
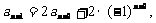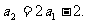　所以　

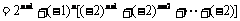
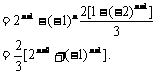
　经验证a₁也满足上式，所以

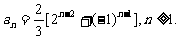
(Ⅲ)证明：

记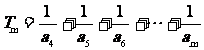

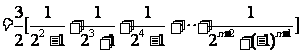
(想用放缩法)

注意到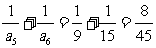

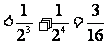. 一般地

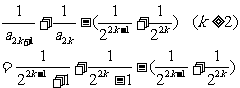
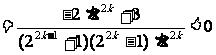
即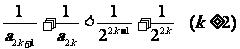

　 ∴当m是奇数时,

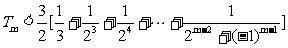
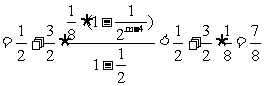
当m是偶数时,再添上第m­­­+1项(放大了)凑够奇数项,利用上述结论可知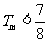也成立,

所以对任意整数m>4，有

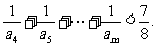
7. (2003福建质检)已知函数f(x)=|log₂(x+1)|，实数m、n在其定义域内，且m＜n，f(m)=f(n).

求证：(1)m+n＞0；

(2)f(m²)＜f(m+n)＜f(n²).

(1)证法一：由f(m)=f(n)，得|log₂(m+1)|=|log₂(n+1)|，即log₂(m+1)=±log₂(n+1)，

log₂(m+1)=log₂(n+1)，　　　　　　　　　　　　　　　　　　　　　 ①

或log₂(m+1)=log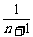₂.　　　　　　　　　　　　　　　　　　　　　　 ②

由①得m+1=n+1，与m＜n矛盾，舍去.

由②得m+1=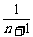，即(m+1)(n+1)=1.　　　　　　　　　　 ③

∴m+1＜1＜n+1.∴m＜0＜n.∴mn＜0.

由③得mn+m+n=0，m+n=－mn＞0.

证法二：(同证法一得)(m+1)(n+1)=1.

∵0＜m+1＜n+1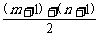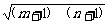，∴＞=1.∴m+n+2＞2.∴m+n＞0.

(2)证明：当x＞0时，f(x)=|log₂(x+1)|=log₂(x+1)在(0，+∞)上为增函数.

由(1)知m²－(m+n)=m²+mn=m(m+n)，且m＜0，m+n＞0，∴m(m+n)＜0.

∴m²－(m+n)＜0，0＜m²＜m+n.

∴f(m²)＜f(m+n).

同理，(m+n)－n²=－mn－n²=－n(m+n)＜0，

∴0＜m+n＜n².∴f(m+n)＜f(n²).

∴f(m²)＜f(m+n)＜f(n²).

6．设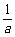+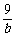=1，a、b∈N^*，则a=.

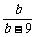∴a+b=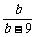+b，b＞9时，

a+b=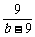+b－9+10≥16.

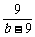=b－9，即b=12取等号，此时a=4.

b＜9无解.∴a=4，b=12.答案：4　 12

[解答题]