
(15) 在复数范围内解方程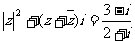 (i为虚数单位).
(i为虚数单位).
(16)已知复数z1满足(1+i)z1=-1+5i, z2=a-2-i, 其中i为虚数单位,a∈R, 若 <
<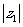 ,求a的取值范围.
,求a的取值范围.
(17) 已知z1, z2是复数, 求证: 若|z1-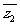 |=|1- z1z2|,则|z1|, |z2|中至少有一个值为1.
|=|1- z1z2|,则|z1|, |z2|中至少有一个值为1.
(18)设复数z1, z2满足z1z2+2i z1-2i z2+1=0.
(Ⅰ)若z1, z2满足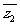 - z1=2i , 求z1, z2;
- z1=2i , 求z1, z2;
(Ⅱ)若|z1|=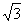 , 是否存在常数k, 使得等式|z2-4 i |=k恒成立, 若存在,试求出k; 若不存在说明理由.
, 是否存在常数k, 使得等式|z2-4 i |=k恒成立, 若存在,试求出k; 若不存在说明理由.
(11)已知复数z1=3+4i, z2=t+i,,且z1·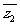 是实数,则实数t等于
.
是实数,则实数t等于
.
(12) 若t∈R, t≠-1, t≠0时,复数z =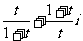 的模的取值范围是 .
的模的取值范围是 .
(13)若a≥0, 且z|z|+az+i=0, 则复数z =
(14)设z=log2(m2-3m-3)+i log2(m-3) (m∈R), 若z对应点在直线x-2y+1=0上, 则m的值是 .
(1)
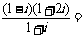 ( )
( )
A.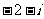 B.
B.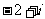 C.
C.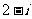 D.
D.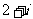
(2) 复数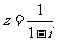 的共轭复数是 (
)
的共轭复数是 (
)
A.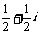 B.
B.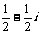 C.
C. D.
D.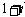
(3) 满足条件|z-i|=|3+4i|复数z在复平面上对应点的轨迹是 ( )
A .一条直线 B .两条直线 C. 圆 D. 椭圆
(4) 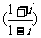 2005 = ( )
2005 = ( )
A.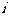 B.-
B.-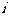 C.
C.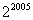 D.-
D.-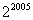
(5) 设z1, z2是复数, 则下列结论中正确的是 ( )
A. 若z12+ z22>0,则z12>- z22 B. |z1-z2|=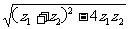
C. z12+
z22=0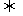 z1=z2=0
D.
|z12|=|
z1=z2=0
D.
|z12|=|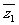 |2
|2
(6)复数z在复平面内对应的点为A, 将点A绕坐标原点, 按逆时针方向旋转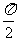 , 再向左平移一个单位, 向下平移一个单位, 得到B点, 此时点B与点A恰好关于坐标原点对称, 则复数z为
( )
, 再向左平移一个单位, 向下平移一个单位, 得到B点, 此时点B与点A恰好关于坐标原点对称, 则复数z为
( )
A. -1 B. 1 C. i D. - i
(7)设复数z =cosθ+icosθ, θ∈[0, π], ω= -1+i, 则|z-ω|的最大值是 ( )
A. 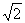 +1
B.
+1
B. 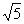 C. 2
D.
C. 2
D. 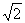
(8) 设z1, z2是非零复数满足z12+ z1z2+
z22=0, 则(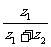 )2+(
)2+(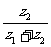 )2的值是
( )
)2的值是
( )
A. -1 B. 1 C. -2 D. 2
(9)已知复数z=x+yi (x,y∈R, x≥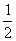 ), 满足|z-1|= x , 那么z在复平面上对应的点(x,y)的轨迹
), 满足|z-1|= x , 那么z在复平面上对应的点(x,y)的轨迹
是 ( )
A. 圆 B. 椭圆 C. 双曲线 D . 抛物线
(10) 设z∈C, 且|z|=1, 当|(z-1)(z-i)|最大时, z = ( )
A . -1
B. - i
C. -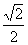 -
-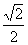 i
D.
i
D. 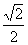 +
+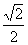 i
i
六,后记
2.掌握两个公式:
1.根式的概念:若n>1且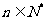 ,则
,则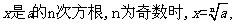
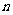 为偶数时,
为偶数时,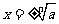 ;
;
3、求值化简: 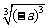 ;
; 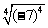 ;
; 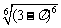 ;
; 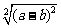 (
(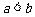 )
)
2、 化简: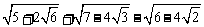 ;
;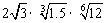
1. 计算或化简: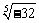 ;
;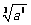 (推广:
(推广: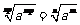 , a
, a 0).
0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com