
6.学校文艺队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有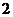 人,会跳舞的有
人,会跳舞的有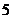 人,现从中选
人,现从中选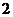 人.设
人.设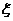 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且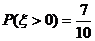 .
.
⑴求文艺队的人数;
⑵写出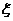 的概率分布列并计算
的概率分布列并计算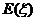 .
.
5. 已知数列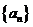 满足
满足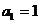 ,且
,且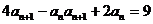
 (
(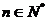 ).
).
⑴求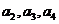 的值;
的值;
⑵由⑴猜想的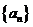 通项公式,并给出证明.
通项公式,并给出证明.
4.(坐标系与参数方程)
从极点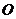 作直线与另一直线
作直线与另一直线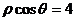 相交于点
相交于点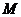 ,在
,在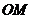 上取一点
上取一点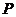 ,使
,使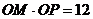 .
.
⑴求点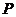 的轨迹方程;
的轨迹方程;
⑵设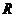 为直线
为直线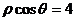 上任意一点,试求
上任意一点,试求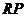 的最小值.
的最小值.
选做第_______题:
选做第_______题:
3.(矩阵与变换)
设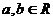 ,若矩阵
,若矩阵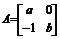 把直线
把直线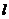 :
: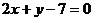 变换为另一直线
变换为另一直线 :
: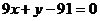 ,求
,求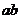 的值.
的值.
2.(不等式选讲)
对于任意的实数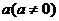 和
和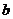 ,不等式
,不等式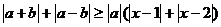 恒成立,试求实数
恒成立,试求实数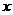 的取值范围.
的取值范围.
1. (几何证明选讲)
(几何证明选讲)
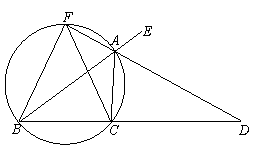
如图,已知AD是ΔABC的外角ÐEAC的平分线,交BC的延长线于点D,延长DA 交ΔABC的外接圆于点F,连结FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是ΔABC外接圆的直径,ÐEAC=120°, BC=6cm,求AD的长.
20. ( 本大题16分,第一小题5分,第二小题5分,第三小题6分)
已知公差大于零的等差数列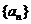 的前n项和为Sn,且满足:
的前n项和为Sn,且满足: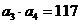 ,
, .
.
(1)求数列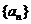 的通项公式
的通项公式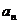 ;
;
(2)若数列 是等差数列,且
是等差数列,且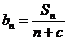 ,求非零常数c;
,求非零常数c;
(3)若(2)中的 的前n项和为
的前n项和为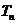 ,求证:
,求证: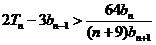
数学附加题
(时间30分钟,满分40分)
19. ( 本大题16分,第一小题5分,第二小题5分,第三小题6分)
如图,已知椭圆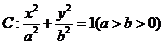 的焦点和上顶点分别为
的焦点和上顶点分别为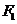 、
、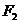 、
、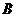 ,我们称
,我们称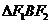 为椭圆
为椭圆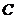 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
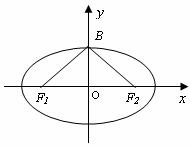 (1)已知椭圆
(1)已知椭圆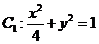 和
和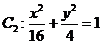 ,判断
,判断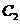 与
与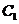 是否
是否
相似,如果相似则求出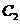 与
与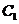 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)写出与椭圆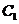 相似且半短轴长为
相似且半短轴长为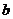 的椭圆
的椭圆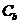 的方程,并列举
的方程,并列举
相似椭圆之间的三种性质(不需证明);
(3)已知直线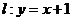 ,在椭圆
,在椭圆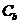 上是否存在两点
上是否存在两点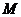 、
、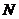 关于直
关于直
线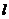 对称,若存在,则求出函数
对称,若存在,则求出函数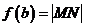 的解析式.
的解析式.
18. ( 本大题15分,第一小题7分,第二小题8分)
⑴在长度为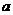 的线段
的线段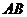 上任意作一点
上任意作一点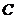 ,求
,求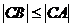 的概率;
的概率;
⑵若将长度为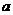 的线段截成三段,则三段长能围成一个三角形的概率有多大.
的线段截成三段,则三段长能围成一个三角形的概率有多大.
17.( 本大题15分,第一小题7分,第二小题8分)
已知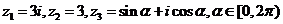 ,
,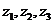 在平面上对应的点
在平面上对应的点
为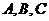 .
.
(1)若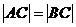 ,求
,求 的值;
的值;
(2)若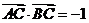 ,求
,求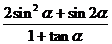 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com