
1. (本题10分)圆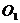
 和圆
和圆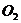 的极坐标方程分别为
的极坐标方程分别为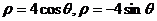 .
.
(1)把圆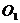
 和圆
和圆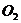 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过圆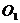
 ,圆
,圆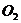 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
20.解 (1)数列
(1)数列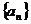 是公差为
是公差为
 的等差数列
的等差数列
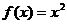 ,且
,且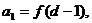
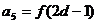
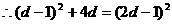
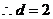
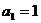
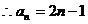 ………………….4分
………………….4分
数列 是公比为
是公比为 的(q∈R)的等比数列
的(q∈R)的等比数列
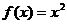 ,且,
,且,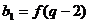 ,
,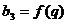
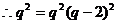
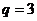
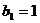
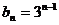 ………………….8分
………………….8分
(2) 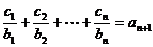
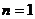
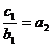
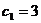 ,
,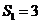 ………………….10分
………………….10分
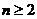
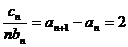
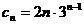 ………………….12分
………………….12分
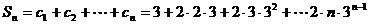
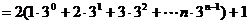
设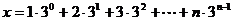

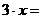
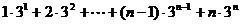
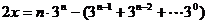
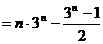
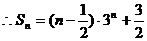 ………………….14分
………………….14分
 综上
综上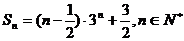 ………………….16分
………………….16分
 泰州实验中学2008-2009学年度第一学期期末考试
泰州实验中学2008-2009学年度第一学期期末考试
高三数学理科附加题 命题人:毛加和
本卷共有4题,解答下列各题必须写出必要的步骤,每题10分.
19、[解](1)当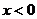 时
时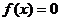 ,当
,当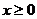 时,
时, . …………….2分
. …………….2分
由条件可知,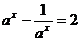 ,即
,即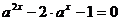 解得
解得 …………6分
…………6分
∵ 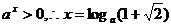 …………..8分
…………..8分
(2)当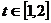 时,
时,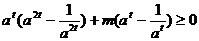 ……………10分
……………10分
即 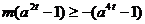
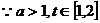
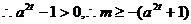 ………………13分
………………13分
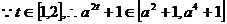
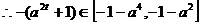
故m的取值范围是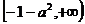 …………….16分
…………….16分
17. .解: (1)
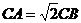 ,
,
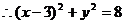 ………………….8分
………………….8分
(2)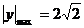 ………………….10分
………………….10分
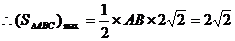 ………………….15分
………………….15分
18解 (1)由表中数据,知
(1)由表中数据,知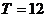 ,
, 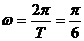
 由
由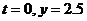 得
得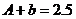
由 ,得
,得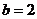

所以,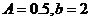 振幅A=
振幅A=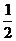 ,∴y=
,∴y=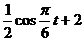 ………………….8分
………………….8分
(2)由题意知,当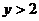 时,才可对冲浪者开放
时,才可对冲浪者开放 ∴
∴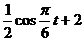 >2,
>2, 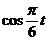 >0
>0
∴–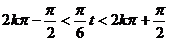 ,
,
即有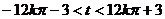 ,
,
由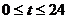 ,故可令
,故可令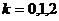 ,得
,得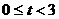 或
或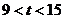 或
或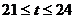
 ……1.4分
……1.4分
∴在规定时间内有6个小时可供游泳爱好者运动即上午9 00至下午15
00至下午15 00
00 ……….15分
……….15分
16.解:(1)取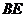 的中点为
的中点为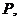 连
连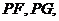 可以证明
可以证明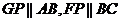
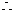 面
面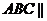 面
面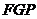 ,
, 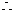
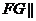 面
面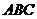 …………………6分
…………………6分
(2)取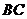 中点
中点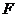 ,连接
,连接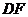 交
交 于点
于点 ,
,
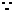
 ,
,
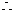
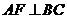 ,
,
又面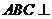 面
面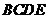 ,
,
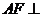 面
面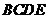 ,
,
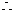
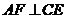 .………………….10分
.………………….10分
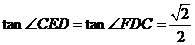 ,
,
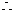
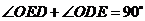 ,
,
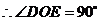 ,即
,即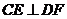 ,
,
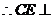 面
面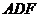 ,
,
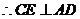 .………………….14分
.………………….14分
15.解:(1)由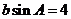 得
得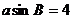 ,
,
由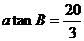 与
与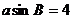 两式相除,有:
两式相除,有:
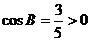 ,
, ………………….4分
………………….4分
又通过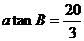 知:
知: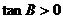 ,
,
则 ,
,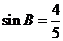 ,
,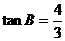
则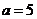 .
. ………………….8分
………………….8分
(2)由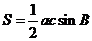 ,得到
,得到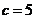 .
.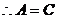
 ………………….10分
………………….10分
由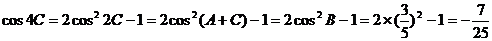
 ….14分
….14分
12. 60
13. 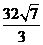 14. 857
14. 857
9. (0,1) 10. 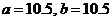 11.
11.
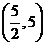 .
.
5. 2
6. -1. 7.
③ 8. 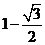
1.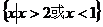 2.
2.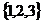 3.
3.
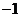 4.
6
4.
6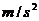
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com