
5.如果实数x,y满足不等式组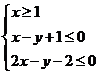 ,则z=x+2y最小值为
.
,则z=x+2y最小值为
.
4.已知向量a=(sinx,cosx),b=(1,一2),且a⊥b,则tan2x= .
3.若命题“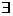 x∈R,x2+ax+1<0”是真命题,则实数a的取值范围是
.
x∈R,x2+ax+1<0”是真命题,则实数a的取值范围是
.
2.在复平面内,复数z= (i是虚数单位)对应的点位于第
象限·
(i是虚数单位)对应的点位于第
象限·
1.已知集合A={x|x=2n-l,n∈Z},B={x|x2一4x<0},则A∩B= .
4.解:(Ⅰ)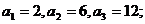 ……………….6分
……………….6分
(2)依题意,得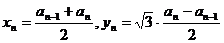 ,由此及
,由此及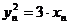 得
得
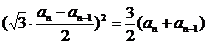 ,
,
即 .
.
由(Ⅰ)可猜想: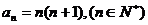 .
.
下面用数学归纳法予以证明:
(1)当 时,命题显然成立;
时,命题显然成立;
(2)假定当 时命题成立,即有
时命题成立,即有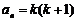 ,则当
,则当 时,由归纳假设及
时,由归纳假设及
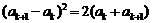
得 ,即
,即
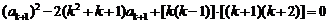 ,
,
解之得
 (
(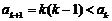 不合题意,舍去),
不合题意,舍去),
即当 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立.……………….10分
3.解法一:
 (1)证明:作
(1)证明:作 交
交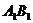 于
于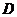 ,连
,连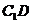 .
.
则 .
.
因为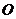 是
是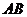 的中点,
的中点,
所以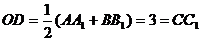 .
.
则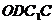 是平行四边形,因此有
是平行四边形,因此有 .
.
 平面
平面 且
且 平面
平面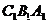 ,
,
则 面
面 .……………….5分
.……………….5分
(2)如图,过 作截面
作截面 面
面 ,分别交
,分别交 于
于 .
.
作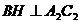 于
于 ,连
,连 .
.
因为 面
面 ,所以
,所以 ,则
,则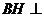 平面
平面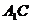 .
.
又因为
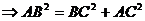 .
.
所以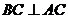 ,根据三垂线定理知
,根据三垂线定理知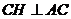 ,所以
,所以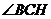 就是所求二面角的平面角.
就是所求二面角的平面角.
因为 ,所以
,所以 ,故
,故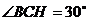 ,
,
即:所求二面角的大小为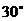 .……………….10分
.……………….10分
解法二:
(1)如图,以 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
 则
则 因为
因为 是
是 的中点,所以
的中点,所以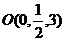 ,
,
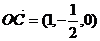 .
.
易知,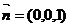 是平面
是平面 的一个法向量.
的一个法向量.
因为
 平面
平面 ,
,
所以 平面
平面 .……………….5分
.……………….5分
(2) ,
,
设 是平面
是平面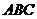 的一个法向量,则
的一个法向量,则
则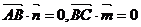 得:
得:
取 .
.
显然, 为平面
为平面 的一个法向量.
的一个法向量.
则 ,结合图形可知所求二面角为锐角.
,结合图形可知所求二面角为锐角.
所以二面角 的大小是
的大小是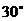 .……………….10分
.……………….10分
4. (本题满分10分)如图,
(本题满分10分)如图,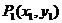 、
、 、…、
、…、
 是曲线
是曲线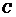 :
: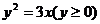 上的
上的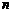 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形(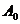 是坐标原点).
是坐标原点).
(Ⅰ)写出 、
、 、
、 ;
;
(Ⅱ)求出点 (
( )的
)的
横坐标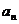 关于
关于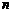 的表达式并证明.
的表达式并证明.
1解:以有点为原点,极轴为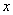 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1) 由
由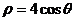 得
得 .
.
所以 .
.
即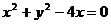 为圆
为圆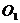 的直角坐标方程.……………….3分
的直角坐标方程.……………….3分
同理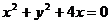 为圆
为圆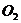 的直角坐标方程.……………….6分
的直角坐标方程.……………….6分
(2)由 解得
解得
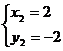 .
.
即圆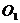 ,圆
,圆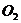 交于点
交于点 和
和 .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为 .……………….10分
.……………….10分
2解:分别记甲、乙、丙经第一次烧制后合格为事件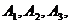
(1)设 表示第一次烧制后恰好有一件合格,则
表示第一次烧制后恰好有一件合格,则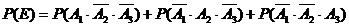
 .……………….5分
.……………….5分
(2)解法一:因为每件工艺品经过两次烧制后合格的概率均为 ,
,
所以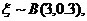
故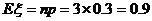 .……………….10分
.……………….10分
解法二:分别记甲、乙、丙经过两次烧制后合格为事件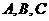 ,
,
则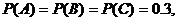
所以
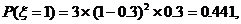
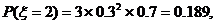

于是 ……………….10分
……………….10分
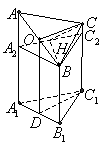
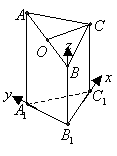
3.(本小题满分10分) 右图是一个直三棱柱(以
右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为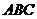 .已知
.已知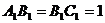 ,
,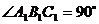 ,
, .
.
(1)设点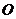 是
是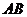 的中点,证明:
的中点,证明: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
2. (本题10分)某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为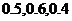 ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为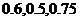 .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为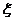 ,求随机变量
,求随机变量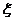 的期望.
的期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com