5．在一个边长为2的正方形中随机撒入200粒豆子，恰有120粒落在阴影区域内，则该阴影部分的面积约为

　 A．　　　　　　 B．

C．　　　　　　 D．

4．名工人某天生产同一零件，生产的件数是设其平均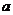数为,中位数为,众数为，则有

A．　　 B． 　　 C．　　 D．

3．如果复数的实部和虚部相等，则实数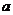等于

A．　　　　　 B．　　　　　　 C．　　　　　　 D．

2．下列函数中，在区间上为增函数且以为周期的函数是

A．　　B．　　C．　D．

1．已知全集，集合，，则

　 A．　　　B．　　　C．　　　D．

22．(本小题满分15分)

　　 如图，F是椭圆(a>b>0)的一个焦点，A,B是椭圆的两个顶点，椭圆的离心率为．点C在x轴上，BC⊥BF，B，C，F三点确定的圆M恰好与直线l₁：相切．

　 (Ⅰ)求椭圆的方程：

　 (Ⅱ)过点A的直线l₂与圆M交于PQ两点，且，求直线l₂的方程．　　

21．(本小题满分15分)

　　 已知二次函数的图像经过坐标原点，其导函数f'(x)=2x+2，数列的前n项和为，点(n，S_n)(n∈N*)均在函数的图像上．

　 (Ⅰ)求数列的通项公式；

　 (Ⅱ)设b_n=，T_n是数列{b_n}的前n项和，求．

20．(本小题满分14分)

　　 已知函数 (a∈R)

　 (Ⅰ)若函数f(x)的图象在x=2处的切线方程为，求a，b的值；

　 (Ⅱ)若函数f(x)在(1，+∞)为增函数，求a的取值范围．

19．(本小题满分14分)

如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，

M为AP的中点．

　 (Ⅰ)求证：DM∥平面PCB；　　　　　　　　

　 (Ⅱ)求直线AD与PB所成角；

　 (Ⅲ)求三棱锥P-MBD的体积．

18．(本小题满分14分)

　　 一袋中有m(m∈N^*)个红球，3个黑球和2个自球，现从中任取2个球．

　 (Ⅰ)当m=4时，求取出的2个球颜色相同的概率；

　 (Ⅱ)当m=3时，设ξ表示取出的2个球中黑球的个数，求ξ的概率分布及数学期望；

　 (Ⅲ)如果取出的2个球颜色不相同的概率小于，求m的最小值．