
5.(2009安徽卷文)“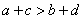 ”是“
”是“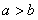 且
且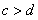 ”的
”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
[解析]易得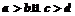 时必有
时必有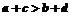 .若
.若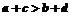 时,则可能有
时,则可能有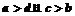 ,选A。
,选A。
[答案]A
4.(2009安徽卷文)不等式组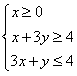 所表示的平面区域的面积等于
所表示的平面区域的面积等于
A. 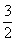 B.
B. 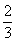
C. 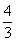 D.
D. 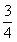
[解析]由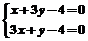 可得
可得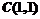 ,故
,故 阴 =
阴 =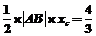 ,选C。
,选C。
[答案]C
3.(2009安徽卷理)若不等式组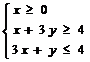 所表示的平面区域被直线
所表示的平面区域被直线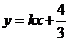 分为面积相等的两部分,则
分为面积相等的两部分,则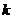 的值是
的值是
 (A)
(A)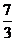 (B)
(B)
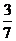 (C)
(C)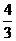 (D)
(D) 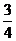
 [解析]:不等式表示的平面区域如图所示阴影部分△ABC
[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由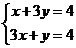 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,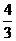 )
)
∴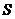 △ABC=
△ABC=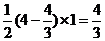 ,设
,设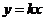 与
与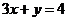 的
的
交点为D,则由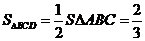 知
知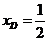 ,∴
,∴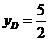
∴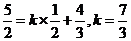 选A。
选A。
2.(2009山东卷理)设x,y满足约束条件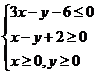 ,
,
若目标函数z=ax+by(a>0,b>0)的值是最大值为12,
则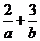 的最小值为( ).
的最小值为( ).
A.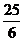 B.
B.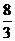 C.
C. 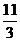 D.
4
D.
4
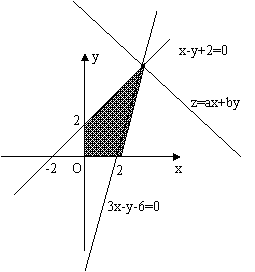
[解析]:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6, 而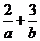 =
=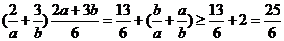 ,故选A.
,故选A.
答案:A
[命题立意]:本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值,对于形如已知2a+3b=6,求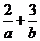 的最小值常用乘积进而用基本不等式解答. .
的最小值常用乘积进而用基本不等式解答. . 

1.(2009安徽卷理)下列选项中,p是q的必要不充分条件的是
(A)p: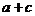 >b+d
, q:
>b+d
, q: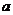 >b且c>d
>b且c>d
(B)p:a>1,b>1 q: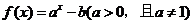 的图像不过第二象限
的图像不过第二象限
(C)p: x=1,
q: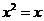
(D)p:a>1,
q: 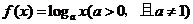 在
在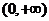 上为增函数
上为增函数
[解析]:由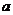 >b且c>d
>b且c>d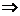
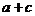 >b+d,而由
>b+d,而由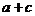 >b+d
>b+d 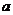 >b且c>d,可举反例。选A
>b且c>d,可举反例。选A
9..(2009湖南卷理)某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__
[答案]:12
[解析]设两者都喜欢的人数为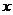 人,则只喜爱篮球的有
人,则只喜爱篮球的有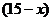 人,只喜爱乒乓球的有
人,只喜爱乒乓球的有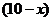 人,由此可得
人,由此可得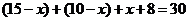 ,解得
,解得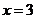 ,所以
,所以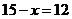 ,即所求人数为12人。.
,即所求人数为12人。. 

8.(2009湖北卷文)设集合A=(x∣log2x<1), B=(X∣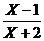 <1), 则A
<1), 则A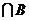 =
.
=
.
[答案]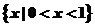 .
. 

[解析]易得A=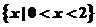 B=
B=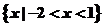 ∴A∩B=
∴A∩B=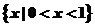 .
.
7.(2009陕西卷文)某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有 人。
答案:8.
解析:由条件知,每名同学至多参加两个小组,故不可能出现一名同学同时参加数学、物理、化学课外探究小组, 设参加数学、物理、化学小组的人数构成的集合分别为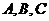 ,则
,则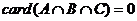 . .
. . 

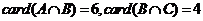 ,
,
由公式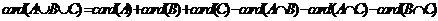
易知36=26+15+13-6-4-
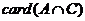 故
故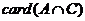 =8 即同时参加数学和化学小组的有8人.
=8 即同时参加数学和化学小组的有8人.
6.(2009天津卷文)设全集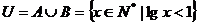 ,若
,若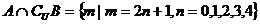 ,则集合B=__________.
,则集合B=__________.
[答案]{2,4,6,8}
[解析]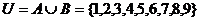
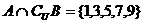
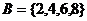
[考点定位]本试题主要考查了集合的概念和基本的运算能力。. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com