15．(2008·辽宁东北育才中学)已知函数f(x)＝ax³+bx²+cx在点x₀处取得极小值－4，使其导数f′(x)>0的x的取值范围为(1,3)，求：

(1) f(x)的解析式；

(2)若过点P(－1，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

解：(1)由题意得：f′(x)＝3ax²+2bx+c＝3a(x－1)(x－3)(a<0)．

∴在(－∞，1)上f′(x)<0；

在(1,3)上f′(x)>0；

在(3，+∞)上f′(x)<0，

因此f(x)在x₀＝1处取得极小值－4，

∴

解方程得

∴f(x)＝－x³+6x²－9x.

(2)设切点Q(t，f(t))，

y－f(t)＝f′(t)(x－t)，

y＝(－3t²+12t－9)(x－t)+(－t³+6t²－9t)

＝(－3t²+12t－9)x+t(3t²－12t+9)－t(t²－6t+9)＝(－3t²+12t－9)x+t(2t²－6t)过(－1，m)，

m＝(－3t²+12t－9)(－1)+2t³－6t².

g(t)＝2t³－3t²－12t+9－m＝0

令g′(t)＝6t²－6t－12＝6(t²－t－2)＝0，求得t＝－1，t＝2，方程g(t)＝0有三个根．需

⇒

⇒故－11<m<16.

因此所求实数m的范围为(－11,16)．

14．已知函数f(x)的图象过点(0,1)，且与函数g(x)＝2x－1－a－1的图象关于直线y＝x－1成轴对称图形．

(1)求函数f(x)的解析式及定义域；

(2)若三个正数m、n、t 依次成等比数列，证明f(m)+f(t)≥2f(n)．

(1)解：在y＝f(x)的图象上取点P(x，y)，设P点关于直线y＝x－1对称的点为Q(m，n)，则

⇒

∵Q在y＝g(x)的图象上，

∴x－1＝2－1－a－1⇒y＝2log₂(x+a)+1.

∵y＝f(x)的图象过点(0,1)，

∴1＝2log₂a+1⇒a＝1.

故f(x)＝2log₂(x+1)+1，定义域为(－1，+∞)．

(2)证明：∵n²＝mt⇒(m+1)(t+1)

＝mt+m+t+1≥n²+2+1

＝(n+1)²，

∴f(m)+f(t)

＝2log₂(m+1)+1+2log₂(t+1)+1

＝2log₂(m+1)(t+1)+2

≥2log₂(n+1)²+2

＝2[2log₂(n+1)+1]＝2f(n)．

13．已知a是实数，函数f(x)＝2ax²+2x－3－a，如果f(x)＝0在区间[－1,1]上有解，求a的取值范围．

解：①若a＝0，f(x)＝2x－3，显然在[－1,1]上没有解，所以a≠0.

令Δ＝4+8a(3+a)＝8a²+24a+4＝0，得a＝，

当a＝时，f(x)＝0恰有一个重根x＝∈[－1,1]．

当a＝时，f(x)＝0恰有一个重根x＝∉[－1,1]．

②当f(－1)f(1)＝(a－1)(a－5)<0，

即1<a<5时，f(x)＝0也恰有一个根在[－1,1]上；

③当f(－1)＝0或f(1)＝0时，有a＝1或a＝5，a＝1时方程恰有一个解，a＝5时方程有两个解，

④当f(x)＝0在[－1,1]上有两个不同解时，则

或

解得a≥5或a<.

因此a的取值范围是a≥1或a≤.

12．(2009·昆明质检)已知函数

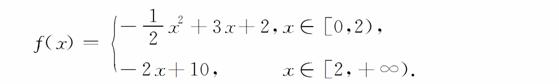
(1)在如下图的坐标系中画出y＝f(x)的图象；

(2)若f(x)>，求x的取值范围．

解：(1)函数的图象如下图．

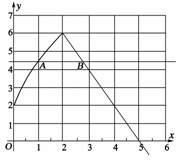
11．(2008·杭州学军中学)记min{a，b}为a，b两数的最小值，当正数x，y变化时，t＝min也在变化，则t的最大值为________．

答案：

解析：x>0，y>0，≤＝，

f(x)=x和g(x)= 的图象如上图，

则t=min的最大值为，故填.

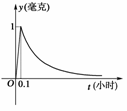
10．为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比；药物释放完毕后，y与t的函数关系式为y＝^t－a(a为常数)，如上图所示．根据图中提供的信息，回答下列问题：

(1)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为__________________________________；

(2)根据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过__________小时后，学生方才能回到教室．

答案：(1)y＝

(2)0.6

解析：本小题主要考查运用函数知识解决实际应用问题的能力．

将(0.1,1)分别代入y＝kt与y＝()^t－a中解得k＝10，

a＝0.1＝

∴y＝

令()t－≤0.25

则2(t－)≥1

解得t≥0.6　即t最小值为0.6.

9．若函数y＝x²+(a+2)x+3，x∈[a，b]的图象关于直线x＝1对称，则b＝________.

答案：6

解析：二次函数y＝x²+(a+2)x+3的图象关于直线x＝1对称，说明二次函数的对称轴为1，即－＝1.∴a＝－4.而f(x)是定义在[a，b]上的，即a、b关于x＝1也是对称的，∴＝1.

∴b＝6.

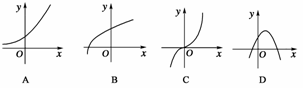
8．(2009·湖北省部分重点中学联考)已知函数y＝f(x)的定义域是R，若对于任意的正数a，函数g(x)＝f(x+a)－f(x)都是其定义域上的增函数，则函数y＝f(x)的图象可能是下图中的(　)

答案：A

解析：在A中图象类似指数函数y=b^x(b>1)的图象，易知g(x)=f(x+a)-f(x)=b^x+a-b^x=b^x(b^a-1)，可知它是单调递增函数，其他几个图象可类似选取适当的函数，易知不合题意．所以选A.

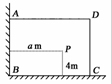
7．(2009·北京市西城区)如右图，有一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别是a m(0<a<12)、4 m，不考虑树的粗细．现在想用16 m长的篱笆，借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S，若将这棵树围在花圃内，则函数S＝f(a) (单位：m²)的图象大致是(　)

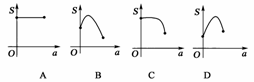
答案：C

解析：由题意，知P(a,4)，设D(x，y)(a≤x<12)，S=xy=x(16-x)=-(x-8)2+64，若0<a≤8，则当x=8时，S取得最大值64；若8<a<12，则当x=a时，S取得最大值-(a-8)2+64，故选C.

6．(2009·北京市东城区)函数y＝f(x)的图象是圆心在原点的单位圆的两段弧(如右图)，则不等式f(x)<f(－x)+2x的解集为(　)

A．{x|－<x<0或<x≤1}

B．{x|－1≤x<－或<x≤1}

C．{x|－1≤x<－或0<x<}

D．{x|－<x<且x≠0}

答案：A

解析：从函数图象可以看出：函数y＝f(x)是关于原点对称的函数，∴f(－x)＝－f(x)；

由不等式f(x)<f(－x)+2x得：f(x)－f(－x)<2x⇒2f(x)<2x⇒f(x)<x，∴y<x；

即函数图象在直线y＝x下方的部分，故选A.