
1、二次函数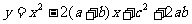 的图像的顶点在x轴上,且a,b,c为
的图像的顶点在x轴上,且a,b,c为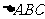 的三边长,则
的三边长,则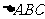 为
为
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)等腰三角形
例1(1)设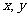 是关于m的方程
是关于m的方程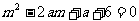 的两个实根,则
的两个实根,则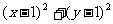 的最小值是
( )
的最小值是
( )
(A)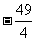 (B)18
(C)8
(D)
(B)18
(C)8
(D)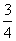
(2)若函数 在区间
在区间 上为减函数,则a的取值范围为( )
上为减函数,则a的取值范围为( )
(A)
(0,1)
(B)( (C)
(C)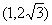 (D)
(D)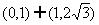
(3)方程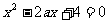 的两根均大于1,则实数a的取值范围是_____。
的两根均大于1,则实数a的取值范围是_____。
例2. (05全国卷Ⅰ)已知二次函数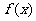 的二次项系数为
的二次项系数为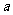 ,且不等式
,且不等式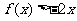 的解集为
的解集为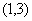 。(Ⅰ)若方程
。(Ⅰ)若方程 有两个相等的根,求
有两个相等的根,求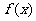 的解析式;
的解析式;
(Ⅱ)若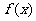 的最大值为正数,求
的最大值为正数,求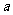 的取值范围。
的取值范围。
例3、不等式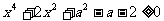 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
例4、设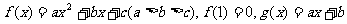
(1)
求证:函数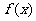 与
与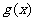 图像有两个交点;
图像有两个交点;
(2)
设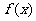 与
与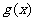 图像交于A,B两点,A,B在x轴上射影为A1,B1,求
图像交于A,B两点,A,B在x轴上射影为A1,B1,求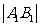 的取值范围;
的取值范围;
(3)
求证:当 时,恒有
时,恒有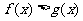
例5. 二次函数f(x)=ax2+bx+c的图象经过点(-1,0),问是否存在常数a、b、c,使x≤f(x)≤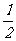 (1+x2)对一切实数都成立?证明你的结论.
(1+x2)对一切实数都成立?证明你的结论.
5、函数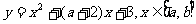 的图像关于直线
的图像关于直线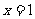 对称,则b=________
对称,则b=________
4、若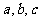 成等比数列,则函数
成等比数列,则函数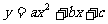 的图像与x轴的公共点个数为_________
的图像与x轴的公共点个数为_________
3、方程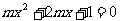 有一根大于1,另一根小于1,则实根m的取值范围是_______
有一根大于1,另一根小于1,则实根m的取值范围是_______
2、已知函数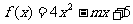 在区间
在区间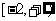 上是增函数,则
上是增函数,则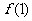 的范围是( )
的范围是( )
(A)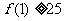 (B)
(B) 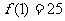 (C)
(C) 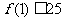 (D)
(D) 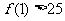
1、二次函数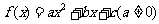 ,若
,若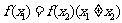 ,则
,则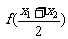 等于( )
等于( )
(A)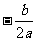 (B)
(B)  (C)
(C)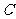 (D)
(D)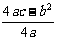
4、 利用二次函数的图像和性质,讨论一元二次方程实根的分布:
设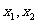 是方程
是方程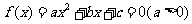 的两个实根,写出下列各情况的充要条件
的两个实根,写出下列各情况的充要条件
①当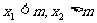 时,_____________________________________________
时,_____________________________________________
②当在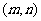 有且只有一个实根时,___________________________________
有且只有一个实根时,___________________________________
③当在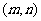 内有两个不相等的实根时,_______________________________
内有两个不相等的实根时,_______________________________
④当两根分别在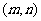 ,
,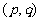 且
且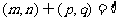 时,________________
时,________________
3、 二次函数与一元一次方程、一元二次不等式之间的内在联系及相应转化
①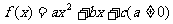 的图像与x轴交点的横坐标是方程f(x)=0的实根;
的图像与x轴交点的横坐标是方程f(x)=0的实根;
②当_______时,f(x)>0恒成立,当_______时,f(x) 0恒成立。结论成立的条件是
0恒成立。结论成立的条件是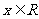 。
。
2、 研究二次函数的图像要抓住开口方向、顶点坐标,讨论二次函数的单调性和最值除抓住开口方向、顶点坐标外,还要抓住对称轴与所给区间的相对位置。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com