
4、若函数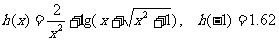 ,则
,则 ( )
( )
(A)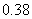 (B)
(B)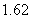 (C)
(C)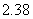 (D)
(D)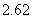
3、设 ,对任意的实数
,对任意的实数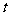 ,都有
,都有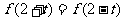 成立,在函数值
成立,在函数值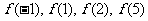 中,最小的一个不可能是
( )
中,最小的一个不可能是
( )
(A)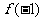 (B)
(B)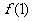 (C)
(C)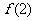 (D)
(D)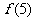
2、若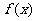 满足
满足 时,恒有
时,恒有 ,则
,则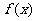 可能是( )
可能是( )
(A) (B)
(B) (C)
(C)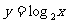 (D)
(D)
1、函数 的图象,可由
的图象,可由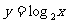 的图象
( )
的图象
( )
A、横坐标不变,纵坐标变为 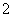 倍而得 B、纵坐标不变,横坐标变为 4倍而得
倍而得 B、纵坐标不变,横坐标变为 4倍而得
C、向上平移2个单位而得 D、向下平移2个单位而得
例1:(1)设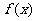 是定义域为R的任一函数,
是定义域为R的任一函数,
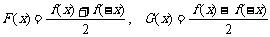 。
。
①判断 与
与 的奇偶性; ②试将函数
的奇偶性; ②试将函数 表示为一个奇函数与一个偶函数的和
表示为一个奇函数与一个偶函数的和
例2:定义在实数集上的函数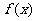 ,对任意
,对任意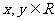 ,有
,有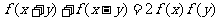 且
且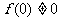 。
。
(1) 求证: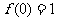
(2)判断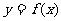 的奇偶性
的奇偶性
(3)若存在正数C,使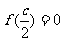 ,①求证对任意
,①求证对任意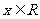 ,有
,有 成立
成立
②试问函数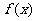 是不是周期函数。如果是,找出它的一个周期;如果不是请证明。
是不是周期函数。如果是,找出它的一个周期;如果不是请证明。
例3:已知函数
(1) 求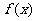 的解析式和定义域
的解析式和定义域
(2) 设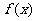 的反函数是
的反函数是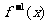 。求证:当
。求证:当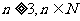 时,
时,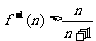 成立
成立
例4:已知奇函数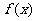 的定义域为R,且
的定义域为R,且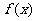 在
在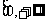 上增函数。当
上增函数。当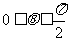 时,是否存在这样的实数
时,是否存在这样的实数 ,使
,使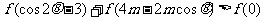 对所有
对所有 均成立?若存在,求所有适合条件的实数
均成立?若存在,求所有适合条件的实数 ,若存在,说明理由。
,若存在,说明理由。
4、若存在常数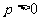 ,使得函数
,使得函数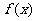 满足
满足 ,则
,则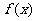 的一个正周期为
的一个正周期为
3、函数 的对称轴为
的对称轴为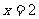 ,则
,则
2、定义在区间 的奇函数
的奇函数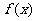 的增函数,偶函数
的增函数,偶函数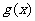 在区间
在区间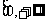 的图象与
的图象与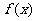 的图象重合。设
的图象重合。设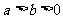 ,给出下列不等式,其中成立的是
( )
,给出下列不等式,其中成立的是
( )
(1)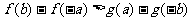 (2)
(2)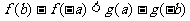
(3)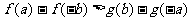 (4)
(4)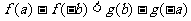
(A)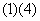 (B)
(B)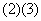 (C)
(C) (D)
(D)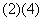
1、不等式 成立的一个充分不必要条件是 ( )
成立的一个充分不必要条件是 ( )
(A) (B)
(B)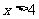 (C)
(C)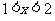 (D)
(D)
3、函数与解析几何知识结合的问题
在解决函数综合问题时,要进行等价转化、分类讨论、数形结合思想的综合运用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com