
例1、①若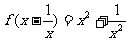 ,则函数
,则函数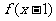 =_____________.
=_____________.
②已知函数 满足
满足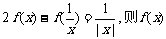 的最小值为
的最小值为 ( )
( )
(A)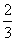 (B)2 (C)
(B)2 (C)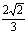 (D)
(D)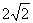
例2、已知f(x)为二次函数,且 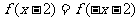 ,且f(0)=1,图象在x轴上截得的线段长为2
,且f(0)=1,图象在x轴上截得的线段长为2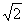 ,求f(x)的解析式 。
,求f(x)的解析式 。
例3、已知函数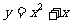 与
与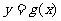 的图象关于点(--2,3)对称,求
的图象关于点(--2,3)对称,求 的解析式。
的解析式。
例4、已知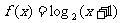 ,当点
,当点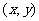 在函数
在函数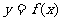 的图象上运动时,点
的图象上运动时,点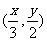 在 函数
在 函数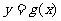 的图象上运动
的图象上运动
(1)
写出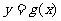 的解析式;
的解析式;
(2)
求出使 的x 的取值范围;
的x 的取值范围;
(3)
在(2)的范围内,求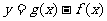 的最大值。
的最大值。
例5.(05江西卷)已知函数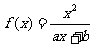 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.(1)求函数f(x)的解析式;
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;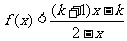 .
.
5、已知f(x)是奇函数,g(x)是偶函数,且f(x)+g(x)= 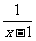 ,则f(x)= ___
,则f(x)= ___
4、若二次函数y=f (x)过点(0,3)、(1,4)、(--1,6),则f (x)=_______________.
3、若一次函数y=f (x)在区间[--1,2]上的最大值为3,最小值为1,则y=f (x)的解析式为_____________.
2、已知 ,则函数
,则函数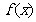 的解析式为
( )
的解析式为
( )
(A)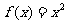 (B)
(B)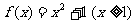
(C)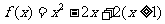 (D)
(D)
1、若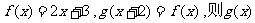 的表达式为
(
)
的表达式为
(
)
(A)2x+1 (B)2x-1 (C)2x-3 (D)2x+7
3、理解轨迹思想在求对称曲线中的应用。
2、求函数的解析式应指明函数的定义域,函数的定义域是使式子有意义的的取值范围,同时也要注意变量的实际意义。
1、求函数解析式的常用方法:
ⅰ、换元法( 注意新元的取值范围)
ⅱ、待定系数法(已知函数类型如:一次、二次函数、反比例函数等)
ⅲ、整体代换(配凑法)
ⅳ、构造方程组(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等)
12、已知函数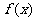 的定义域为
的定义域为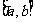 ,且
,且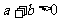 ,求下列各函数的定义域:
,求下列各函数的定义域:
(1)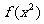 ;
;
(2)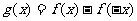 ;
;
(3)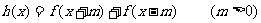
答案:
基本训练:1、A 2、C 3、C 4、A 5、{x|x<0}. 6、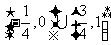
例题:1(1)12 (2)2,1 2(1)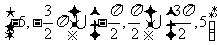 (2)
(2)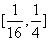 (3)[1,
9] 变题:
(3)[1,
9] 变题: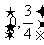 3(1)[-2,2] (2)
3(1)[-2,2] (2) 4(1)
4(1) ,
, 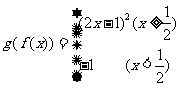 变题1、
变题1、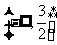 2、
2、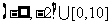 (2)
(2)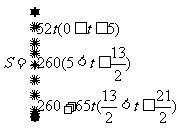 5(1)
5(1)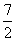 (2)15
(2)15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com