
445. 如图9-29,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB、PC的中点.求证:MN⊥AB.
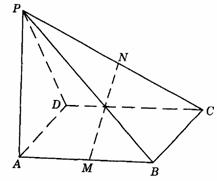
图9-29
解析:连结AC,取AC中点O,连结OM,ON.由OM∥BC,得OM⊥AB.又NO∥PA,且PA⊥AB,故NO⊥AB.由此可得AB⊥平面OMN.因此MN⊥AB.
444. 已知正方体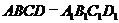 .则
.则
(1) 与平面ABCD所成的角等于________;
与平面ABCD所成的角等于________;
(2)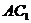 与平面ABCD所成的角的正切值等于________;
与平面ABCD所成的角的正切值等于________;
(3) 与平面
与平面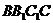 所成的角等于________ ;
所成的角等于________ ;
(4)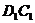 与平面
与平面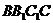 所成的角等于________;
所成的角等于________;
(5)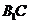 与平面
与平面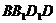 所成的角等于________.
所成的角等于________.
解析:(1)∵
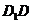 ⊥平面ABCD,∴
⊥平面ABCD,∴
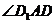 为
为 与平面ABCD所成的角,
与平面ABCD所成的角,
=45°.
(2)∵ 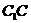 ⊥平面ABCD,∴
⊥平面ABCD,∴
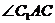 为
为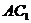 与平面ABCD所成的角.设
与平面ABCD所成的角.设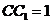 ,则
,则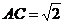 ,∴
,∴ 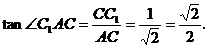
(3)∵ 
 平面
平面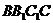 ,
,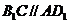 ,∴
,∴  ∥平面
∥平面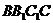 ,∴
,∴  与平面
与平面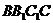 所成的角为0°.
所成的角为0°.
(4)∵ 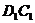 ⊥平面
⊥平面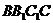 ,∴
,∴ 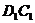 与平面
与平面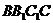 所成的角为90°.
所成的角为90°.
(5)连结AC,交AD于H.连结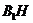 ,∵
,∵ 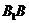 ⊥平面ABCD,CH
⊥平面ABCD,CH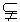 平面ABCD,
平面ABCD,
∴
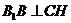 ,又∵ CH⊥BD,∴
CH⊥平面
,又∵ CH⊥BD,∴
CH⊥平面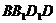 .∴
.∴ 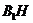 为
为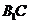 在平面
在平面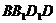 内的射影.∴
内的射影.∴ 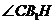 为
为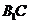 与平面
与平面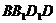 所成的角.设正方体棱长为1,则
所成的角.设正方体棱长为1,则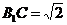 ,
,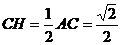 ,∴
,∴ 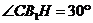 ,即
,即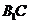 与平面
与平面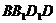 所成的角为30°.
所成的角为30°.
443. 设正方体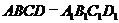 的棱长为1,则
的棱长为1,则
(1)A到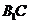 的距离等于________;
的距离等于________;
(2)A到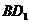 的距离等于________;
的距离等于________;
(3)A到平面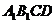 的距离等于________;
的距离等于________;
(4)AB到平面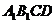 的距离等于________.
的距离等于________.
解析:1)连接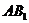 ,AC,则
,AC,则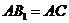 ,取
,取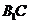 的中点E,连结AE,则
的中点E,连结AE,则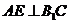 .
.
∴
AE为点A到直线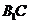 的距离,在Rt△ACE中,
的距离,在Rt△ACE中,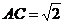 ,
,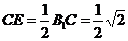 ,
,
∴ 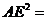
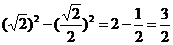 ,∴
,∴ 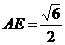 .即A到
.即A到 、C的距离等于
、C的距离等于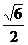 .
.
(2)连结 .∵ AB⊥平面
.∵ AB⊥平面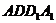 ,∴
,∴ 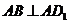 .在Rt△
.在Rt△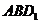 中,AB=1,
中,AB=1, ,
,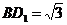 ,设A到
,设A到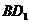 的距离为h,则
的距离为h,则 .即
.即
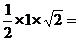
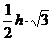 ,∴
,∴ 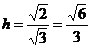 ,即点A到
,即点A到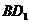 的距离为
的距离为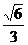 .
.
(3)连结 交
交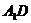 于F,则
于F,则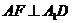 .∵ CD⊥平面
.∵ CD⊥平面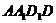 ,且AF
,且AF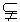 平面
平面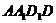 ,∴ CD⊥AF.∵
CD∩AD=D,∴ AF⊥平面
,∴ CD⊥AF.∵
CD∩AD=D,∴ AF⊥平面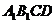 .∴ AF为点A到平面
.∴ AF为点A到平面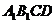 的距离.∵
的距离.∵  ,∴
,∴ 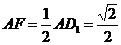 .
.
(4)∵ AB∥CD,∴
AB∥平面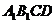 ,∴ AB到平面
,∴ AB到平面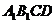 的距离等于A点
的距离等于A点
到平面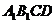 的距离,等于
的距离,等于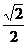 .
.
442. 下列命题中正确的是( ).
A.若a是平面a 的斜线,直线b垂直于a在平面a 内的射影为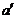 ,则a⊥b
,则a⊥b
B.若a是平面a 的斜线,平面b 内的直线b垂直于a在平面a 内的射影为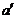 ,则a ⊥b
,则a ⊥b
C.若a是平面a 的斜线,直线b平行于平面a ,且b垂直于a在平面a 内的射影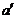 ,则a⊥b
,则a⊥b
D.若a是平面a 的斜线,b是平面a 内的直线,且b垂直于a在另一个平面b 内的射影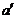 ,则a⊥b
,则a⊥b
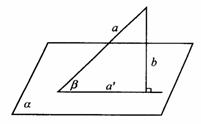
解析:C.如图答9-18,直线b垂直于a在平面a 内的射影,但不能得出a⊥b的结论.排除A.令b 是直线a与其在a 内的射影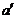 确定的平面,在b 内取垂直于
确定的平面,在b 内取垂直于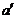 的直线为b,不能得出a⊥b的结论.排除B.同理排除D.如图答9-19,在a 内任取点P,∵
的直线为b,不能得出a⊥b的结论.排除B.同理排除D.如图答9-19,在a 内任取点P,∵ 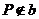 ,则过b与P确定平面g ,设
,则过b与P确定平面g ,设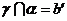 ,因为b∥a ,则
,因为b∥a ,则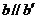 .∵
.∵ 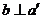 ,∴
,∴ 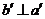 .∴
.∴ 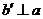 ,∴ b⊥a.于是C正确.
,∴ b⊥a.于是C正确.
441. 已知直线PG⊥平面a 于G,直线EF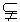 a ,且PF⊥EF于F,那么线段PE、PF、PG的关系是( ).
a ,且PF⊥EF于F,那么线段PE、PF、PG的关系是( ).
A.PE>PG>PF B.PG>PF>PE
C.PE>PF>PG D.PF>PE>PG
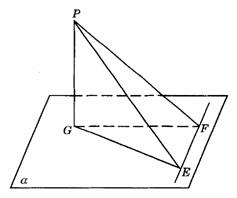
解析:C.如图答9-17.PG⊥a ,EF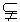 a ,PF⊥EF,则GF⊥EF.在Rt△PGF中,PF为斜边,PG为直角边,PF>PG.在Rt△PFE中,PF为直角边,PE为斜边,PE>PF,所以有PE>PF>PG.
a ,PF⊥EF,则GF⊥EF.在Rt△PGF中,PF为斜边,PG为直角边,PF>PG.在Rt△PFE中,PF为直角边,PE为斜边,PE>PF,所以有PE>PF>PG.
440. ABCD是平面a 内的一个四边形,P是平面a 外的一点,则△PAB、△PBC、△PCD、△PDA中是直角三角形的最多有( ).
A.1个 B.2个 C.3个 D.4个
解析:D.作矩形ABCD,PA⊥平面AC,则所有的三角形都是直角三角形
439. 直线a、b均在平面a 外,若a、b在平面a 上的射影是两条相交直线,则a和b的位置关系是( ).
A.异面直线 B.相交直线 C.平行直线 D.相交或异面直线
解析:D
438. 若直线l与平面a 所成角为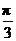 ,直线a在平面a 内,且与直线l异面,则直线l与直线a所成的角的取值范围是( ).
,直线a在平面a 内,且与直线l异面,则直线l与直线a所成的角的取值范围是( ).
A.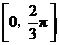 B.
B.
C.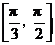 D.
D.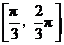
解析:C.因为直线l是平面的斜线,斜线与平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角,故a与l所成的角大于或等于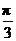 ;又因为异面直线所成的角不大于
;又因为异面直线所成的角不大于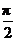 ,故选C.
,故选C.
437. 已知a、b是异面直线,那么经过b的所在平面中( ).
A.只有一个平面与a平行 B.有无数个平面与a平行
C.只有一个平面与a垂直 D.有无数个平面与a垂直
解析:A.过b上任一点P作直线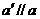 ,由
,由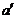 和b确定的平面a 与a平行,这个平面是过b且平行于a的唯一一个平面.故排除B.当a与b不垂直时,假设存在平面b ,使b
和b确定的平面a 与a平行,这个平面是过b且平行于a的唯一一个平面.故排除B.当a与b不垂直时,假设存在平面b ,使b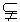 b ,且a⊥b ,则a⊥b,这与a、b不垂直矛盾,所以当a、b不垂直时,不存在经过b且与a垂直的平面,当a、b垂直时,过b且与a垂直的平面是唯一的,设a、b的公垂线为c,则由c和b所确定的平面与a垂直,且唯一.
b ,且a⊥b ,则a⊥b,这与a、b不垂直矛盾,所以当a、b不垂直时,不存在经过b且与a垂直的平面,当a、b垂直时,过b且与a垂直的平面是唯一的,设a、b的公垂线为c,则由c和b所确定的平面与a垂直,且唯一.
436. 空间四边形ABCD的四条边相等,那么它的两条对角线AC和BD的关系是( ).
A.相交且垂直 B.相交但不垂直
C.不相交也不垂直 D.不相交但垂直
解析:D.取BD中点O,则BD⊥AO,BD⊥CO,故BD⊥平面ACO,因此BD⊥AC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com