19．(本小题满分12分)已知点(x，y)在曲线C上，将此点的纵坐标变为原来的2倍，对应的横坐标不变，得到的点满足方程x²+y²＝8；定点M(2,1)，平行于OM的直线l在y轴上的截距为m(m≠0)，直线l与曲线C交于A，B两个不同点．

(1)求曲线C的方程；

(2)求m的取值范围．

解：(1)在曲线C上任取一个动点P(x，y)，　

则点(x,2y)在圆x²+y²＝8上．

所以有x²+(2y)²＝8.

整理得曲线C的方程为+＝1.

(2)∵直线l平行于OM，且在y轴上的截距为m，

又k_OM＝，

∴直线l的方程为y＝x+m.

由得x²+2mx+2m²－4＝0

∵直线l与椭圆交于A、B两个不同点，

∴Δ＝(2m)²－4(2m²－4)>0，

解得－2<m<2且m≠0.

∴m的取值范围是－2<m<0或0<m<2.

18．(本小题满分12分)在直角坐标系xOy中，以O为圆心的圆与直线x－y＝4相切．

(1)求圆O的方程；

(2)圆O与x轴相交点A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求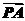·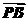的取值范围．

解：(1)依题设，圆O的半径r等于原点O到直线x－y＝4的距离，即r＝＝2.

得圆O的方程为x²+y²＝4.

(2)不妨设A(x_1,0)，B(x_2,0)，x₁＜x₂.

由x²＝4即得A(－2,0)，B(2,0)．

设P(x，y)，由|PA|、|PO|、|PB|成等比数列，得

·＝x²+y²，

即x²－y²＝2.

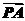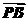·＝(－2－x，－y)·(2－x，－y)＝x²－4+y²

＝2(y²－1)．

由于点P在圆O内，故由此得y²＜1.

所以·的取值范围为[－2,0)．

17．(本小题满分12分)已知A(x₁，y₁)，B(x₂，y₂)分别在直线x+y－7＝0及x+y－5＝0上，求AB中点M到原点距离的最小值．

解：设AB中点为(x₀，y₀)，

∴

又∵

∴(x₁+x₂)+(y₁+y₂)＝12，

∴2x₀+2y₀＝12，

∴x₀+y₀＝6.

∴原点到x₀+y₀＝6距离为所求，即d＝＝3.

16．(2009·湖南高考)过双曲线C：－＝1(a＞0，b＞0)的一个焦点作圆x²+y²＝a²的两条切线，切点分别为A，B.若∠AOB＝120°(O是坐标原点)，则双曲线C的离心率为________．

解析：∵∠AOB＝120°，∴∠AOF＝60°.

在Rt△OAF中，|OA|＝a，|OF|＝c，

∴e＝＝＝＝2.

答案：2

15．(2009·全国卷Ⅱ)已知圆O：x²+y²＝5和点A(1,2)，则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于________．

解析：依题意过A(1,2)作圆x²+y²＝5的切线方程为x+2y＝5，在x轴上的截距为5，在y轴上的截距为，切线与坐标轴围成的面积S＝··5＝.

答案：

14．设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长，则直线x·sinA+ay+c＝0与bx－y·sinB+sinC＝0的位置关系是________．

解析：在△ABC中，由正弦定理得＝，

∴asinB－bsinA＝0，

∴两直线垂直．

答案：垂直

13．(2009·杭州模拟)直线x+2y－2＝0经过椭圆+＝1(a>b>0)的一个焦点和一个顶点，则该椭圆的离心率等于________．

解析：直线过点(2,0)和(0,1)，即为椭圆的一个焦点和一个顶点，又a>b>0，∴焦点在x轴上，

∴c＝2，b＝1，a＝＝，∴e＝.

答案：

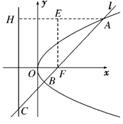
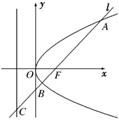
12．(2010·诸城模拟)过抛物线y²＝2px(p>0)的焦点F的

直线l交抛物线于点A、B(如图所示)，交其准线于点C，

若|BC|＝2|BF|，且|AF|＝3，则此抛物线的方程为 (　)

A．y²＝9x　　　　 　B．y²＝6x

C．y²＝3x　　　　　 D．y²＝x

解析：点F到抛物线准线的距离为p，又由|BC|＝2|BF|得点

B到准线的距离为|BF|，则＝，∴l与准线夹角为30°，

则直线l的倾斜角为60°.由|AF|＝3，如图连结AH⊥HC，

EF⊥AH，则AE＝3－p，

则cos60°＝，故p＝.

∴抛物线方程为y²＝3x.

答案：C

11．若直线ax+by+1＝0(a、b>0)过圆x²+y²+8x+2y+1＝0的圆心，则+的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．8　 　　　　　　B．12 　　　　　　　　C．16 　　　　　　　D．20

解析：由题意知，圆心坐标为(－4，－1)，由于直线过圆心，所以4a+b＝1，从而+＝(+)(4a+b)＝8++≥8+2×4＝16(当且仅当b＝4a时取“＝”)．

答案：C

10．抛物线y²＝2px(p>0)的准线经过等轴双曲线x²－y²＝1的左焦点，则p＝(　)

A. 　　　　　　　B.　　　　　　　 C．2 　　　　　　　D．4

解析：双曲线x²－y²＝1的左焦点为(－，0)，故抛物线的准线为x＝－，∴＝，p＝2.

答案：C