24. The hunter calmly picked up his gun,took the aim and fired, ______ the beast.

　　 A.bringing down B.pulling down　 C.falling dowing　 D.putting down

23.Hearing that most of the members voted against her, she ______ a smiile.

　　 A.wore　　　　 B. managed　　 C.performed　　trolled

22. It is a strange phenomenon that some young people today think it is their parents’responsibility to earn money and_______ to spend it.

　　 A.them　　　　 B.they　　　　 C.their　　　　 D.theirs

第一节　　　　 单项填空(共15小题；每小题1分，满分15分)

从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

21.. Department of Homeland Security and CIA produced ______ joint report on Monday warning that ______ next 911 could in fact occur on ______ different date.

　　 A.the; a; the　 　B.a; the; a　　 C./; the; the　　 D.a; /; the

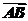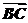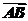22．(本小题满分14分)已知△ABC的面积为S，满足≤S≤3，且·＝6， 与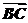的夹角为θ.

(1)求角θ的取值范围；

(2)求函数f(θ)＝sin²θ+2sinθ·cosθ+3cos²θ的最小值．

解：(1)由题意知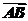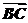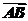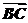，·＝| |·| |cosθ＝6，　　　　　　　　　　　 ①

S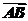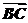＝||·||sin(π－θ)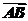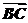＝||·||sinθ，　　　　　　　　　　　　　　 ②

由，得＝tanθ，即3tanθ＝S.

由≤S≤3，得≤3tanθ≤3，

即≤tanθ≤1.

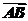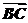又θ为与的夹角，

∴θ∈(0，π]，∴θ∈[，]．

(2)f(θ)＝sin²θ+2sinθ·cosθ+3cos²θ

＝1+sin2θ+2cos²θ

＝2+sin2θ+cos2θ

＝2+sin(2θ+)．

∵θ∈[，]，∴2θ+∈[，]，

∴当2θ+＝，即θ＝时，f(θ)取得最小值为3.

21．(本小题满分12分)已知向量a＝(cosx，sinx)，b＝(－cosx，cosx)，c＝(－1,0)．

(1)若x＝，求向量a，c的夹角；

(2)当x∈[，]时，求函数f(x)＝2a·b+1的最大值．

解：(1)设a，c的夹角为θ，当x＝时，

cos〈a，c〉＝＝

＝－cosx＝－cos＝cos.

∵0≤〈a，c〉≤π，∴〈a，c〉＝.

(2)f(x)＝2a·b+1＝2(－cos²x+sinxcosx)+1

＝2sinxcosx－(2cos²x－1)＝sin2x－cos2x

＝sin(2x－)．

∵x∈[，]，

∴2x－∈[，2π]，

∴sin(2x－)∈[－1，]，

∴当2x－＝，即x＝时，f(x)_max＝1.

20．(本小题满分12分)在△ABC中，角A、B、C所对的边长分别为a、b、c，已知向量m＝(1,2sinA)，n＝(sinA,1+cosA)，且满足m∥n，b+c＝a.

(1)求角A的大小；

(2)求sin的值．

解：(1)∵m∥n，∴1+cosA＝2sin²A，

即2cos²A+cosA－1＝0，解得cosA＝－1(舍去)，cosA＝.

又0＜A＜π，∴A＝.

(2)∵b+c＝a，

∴由正弦定理可得sinB+sinC＝sinA＝.

又C＝π－(A+B)＝－B，∴sinB+sin＝，

即sinB+cosB＝，∴sin＝.

19．(本小题满分12分)已知向量a＝(cos(－θ)，sin(－θ))，b＝(cos(－θ)，sin(－θ))．

(1)求证：a⊥b；

(2)若存在不等于0的实数k和t，使x＝a+(t²+3)b，

y＝－ka+tb，满足x⊥y，试求此时的最小值．

解：(1)证明：∵a·b

＝cos(－θ)·cos(－θ)+sin(－θ)·sin(－θ)

＝sinθcosθ－sinθcosθ＝0.

∴a⊥b.

(2)由x⊥y得：x·y＝0，

即[a+(t²+3)b]·(－ka+tb)＝0，

∴－ka²+(t³+3t)b²+[t－k(t²+3)]a·b＝0，

∴－k|a|²+(t³+3t)|b|²＝0.

又|a|²＝1，|b|²＝1，

∴－k+t³+3t＝0，∴k＝t³+3t.

∴＝＝t²+t+3＝(t+)²+.

故当t＝－时，有最小值.