
例1  如图已知
如图已知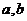 是两条异面直线,所成的角为
是两条异面直线,所成的角为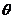 ,点
,点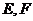 分别在直线
分别在直线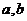 上,线段
上,线段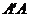 是公垂线段,且
是公垂线段,且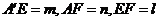 ,求线段
,求线段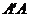 的长
的长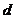 .
.
解: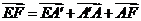
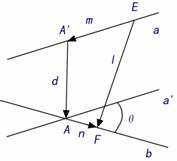 ∴
∴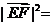
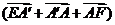
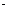
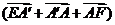
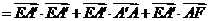
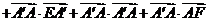
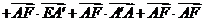
∵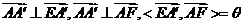 或
或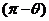
∴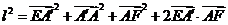
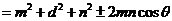 ,
,
所以,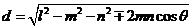 .
.
说明:(1)由上例: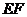 的长是异面直线上任意两点的距离,
的长是异面直线上任意两点的距离,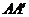 的长是异面直线的距离;
的长是异面直线的距离;
(2)当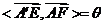 时,
时,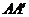 的长的运算中取"-".
的长的运算中取"-".
例2.已知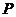 是
是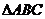 所在平面外的一点,
所在平面外的一点,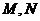 分别是
分别是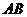 和
和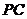 的中点,
的中点,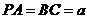 ,
,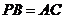 ,
,
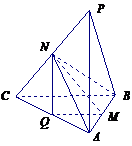 (1)求证:
(1)求证: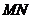 是
是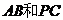 的公垂线;
的公垂线;
(2)当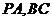 成
成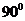 角时,求
角时,求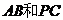 间的距离
间的距离
解:(1)连结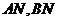 ,
,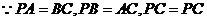 ,
,
∴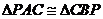 ,∵
,∵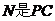 的中点,∴
的中点,∴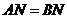 ,
,
又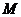 是
是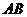 的中点,∴
的中点,∴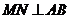 ,同理:
,同理: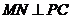 ,
,
∴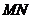 是
是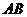 和
和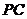 的公垂线
的公垂线
(2)取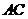 的中点
的中点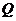 ,连结
,连结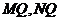 ,∵
,∵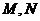 分别是
分别是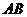 和
和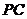 的中点,
的中点,
∴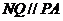 ,
,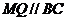 ,
,
∴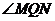 是异面直线
是异面直线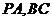 所成的角,即
所成的角,即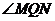
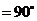 ,
,
且可得: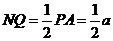 ,
,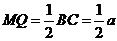 ,
,
∴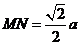 ,即
,即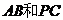 间的距离为
间的距离为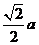 .
.
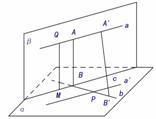
例3.如图直二面角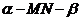 中,
中,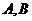 两点分别在平面
两点分别在平面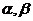 内,
内,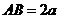 ,
,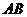 与平面
与平面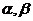 所成的角分别是
所成的角分别是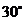 和
和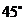 ,求
,求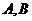 两点在棱
两点在棱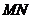 上的射影间的距离
上的射影间的距离
解:作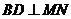 于
于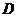 ,
,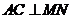 于
于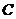 ,连结
,连结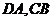 ,
,
∵二面角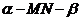 是直二面角,∴平面
是直二面角,∴平面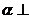 平面
平面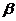 ,
,
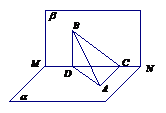 ∴
∴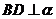
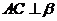 ,
,
∴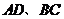 分别是
分别是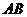 在平面
在平面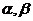 内的射影,
内的射影,
∴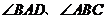 分别是
分别是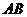 与平面
与平面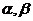 所成的角,
所成的角,
∴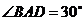 ,
,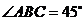 ,∵
,∵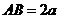 ,∴
,∴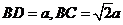 ,
,
∴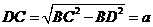 ,即
,即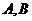 两点在棱
两点在棱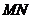 上的射影间的距离为
上的射影间的距离为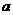 .
.
5.两条异面直线的距离:两条异面直线的公垂线段的长度
说明:两条异面直线的距离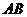 即为直线
即为直线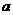 到平面
到平面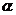 的距离
的距离 即两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离
即两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离
4.公垂线段最短:两条异面直线的公垂线段是分别连结两条异面直线上两点的线段中最短的一条;
3.两条异面直线的公垂线段:两条异面直线的公垂线夹在异面直线间的部分,叫做两条异面直线的公垂线段;
1  异面直线的公垂线:和两条异面直线都垂直相交的直线叫做异面直线的公垂线.
异面直线的公垂线:和两条异面直线都垂直相交的直线叫做异面直线的公垂线.
2.公垂线唯一:任意两条异面直线有且只有一条公垂线
证明:设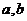 是两条异面直线.在
是两条异面直线.在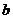 上任取一点
上任取一点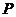 ,过
,过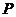 引
引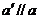 ,
,
设 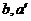 确定平面
确定平面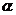 ,则
,则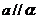 .在
.在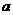 上任取一点
上任取一点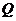 ,过
,过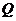 引
引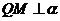 ,
,
垂足为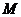 ,设
,设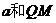 确定的平面
确定的平面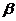 与平面
与平面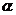 相交于直线
相交于直线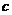 ,
,
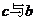 相交于点
相交于点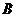 ,在
,在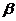 内作
内作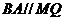 ,交
,交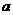 于点
于点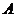 ,
,
则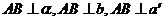 ,又∵
,又∵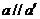 ,∴
,∴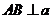 ,
,
∴ 的公垂线段,
的公垂线段,
如果还有直线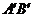 也是
也是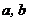 的公垂线,
的公垂线,
则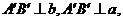 于是
于是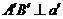 ,
,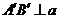 ,
,
∴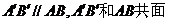 ,即
,即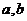 共面,这与
共面,这与 是两条异面直线矛盾,
是两条异面直线矛盾,
所以,两条异面直线的公垂线只有一条
4.两个平行平面的距离:两个平行平面的公垂线段的长度叫做两个平行平面的距离
3.两个平行平面的公垂线、公垂线段:
(1)两个平面的公垂线:和两个平行平面同时垂直的直线,叫做两个平面的公垂线
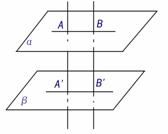 (2)两个平面的公垂线段:公垂线夹在平行平面间的的部分,叫做两个平面的公垂线段
(2)两个平面的公垂线段:公垂线夹在平行平面间的的部分,叫做两个平面的公垂线段
(3)两个平行平面的公垂线段都相等
(4)公垂线段小于或等于任一条夹在这两个平行平面间的线段长
2.直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离(转化为点面距离)
1.点到平面的距离:
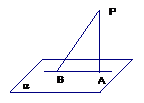 已知点
已知点 是平面
是平面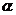 外的任意一点,过点
外的任意一点,过点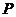 作
作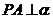 ,垂足为
,垂足为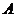 ,则
,则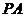 唯一,则
唯一,则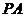 是点
是点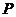 到平面
到平面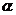 的距离
的距离
即:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离 (转化为点到点的距离)
(转化为点到点的距离)
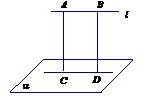 结论:连结平面
结论:连结平面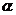 外一点
外一点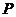 与
与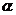 内一点所得的线段中,垂线段
内一点所得的线段中,垂线段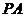 最短
最短
2.) 忠诚;挚爱,热爱[U][(+to/for)]
devotion to music 热爱音乐
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com