7. [2010·全国卷Ⅱ]I’m afraid Mr. Harding_________see you now. He’s busy.

’t　 　　　B.mustn’t　 　　　C.shouldn’t　 　　　　D.needn’t

6.(基础题) -What’s going on?

　-______　

A. No, we won’t go on. We need rest.

B. The Times Theatre is on fire.

C. I’m going on telling the story.

D. How about some ice cream?

5. unite　　 　　A. bridge　 　　B. unit　　　 　C. service　　 　D. price

第二节　 语法和词汇知识(共15小题；每小题1分，满分15分)

4. bench　　 　　A. school　 　　B. machine　　 　C. march　　 　　D. character

3. society　 　　A. science　 　　B. convenient　 　C. field　　 　　D. believe

2. visitor　　　　 A. basin　 　　B. measure　　 　C. thirsty　　 　D. cousin

第一节　 (2010·石家庄质检1)语音知识(共5小题；每小题1分，满分5分)

从A、B、C、D四个选项中，找出其划线部分与所给单词的划线部分读音相同的选项，并在答题卡上将该项涂黑。

1. public　　 　　A. argue　 　　B. custom　 　　C. popular　　 　D. busy

12.某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时，可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元，未租出的车每辆每月需要维护费50元.　

(1)当每辆车的月租金定为3 600元时，能租出多少辆车？　

(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？　

解 (1)当每辆车的月租金定为3 600元时，未租出的车辆数为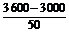=12，所以这时租出了88辆车.

(2)设每辆车的月租金定为x元，则租赁公司的月收益为f(x)=(100-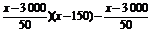×50.

整理得f(x)=-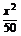 +162x-21 000=-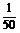(x-4 050)²+307 050.　

所以，当x=4 050时，f(x)最大，最大值为f(4 050)=307 050.

即当每辆车的月租金定为4 050元时，租赁公司的月收益最大，最大月收益为307 050元.

11.如图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径,且上底

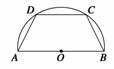CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域.　

解 　AB=2R，C、D在⊙o的半圆周上，　

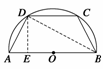设腰长AD=BC=x，作DE⊥AB，　

垂足为E，连接BD，　

那么∠ADB是直角，

由此Rt△ADE∽Rt△ABD.　

∴AD²=AE×AB，即AE=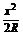，∴CD=AB-2AE=2R-，　

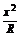所以y=2R+2x+(2R-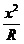),　即y=-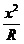+2x+4R.　

再由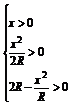,解得0＜x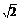＜R.　所以y=-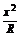+2x+4R,定义域为(0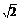，R).

10．(1)设f(x)是定义在实数集R上的函数，满足f(0)=1,且对任意实数a、b,有f(a-b)=f(a)-b(2a-b+1),求f(x);

(2)函数f(x) (x∈(-1,1))满足2f(x)-f(-x)=lg(x+1),求f(x).　

解 (1)依题意令a=b=x,则　

f(x-x)=f(x)-x(2x-x+1),　

即f(0)=f(x)-x²-x,　

而f(0)=1,∴f(x)=x²+x+1.　

(2)以-x代x,依题意有　

2f(-x)-f(x)=lg(1-x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　①　

又2f(x)-f(-x)=lg(1+x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②　

两式联立消去f(-x)得　

3f(x)=lg(1-x)+2lg(1+x),　

∴f(x)=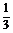lg(1+x-x²-x³)(-1＜x＜1).