
11.(2008·海南、宁夏,21,(1)(3)问)设函数f(x)=ax+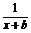 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
(1)解 f′(x)=a-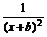 ,
,
于是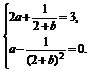
解得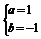 或
或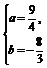
因为a,b∈Z,故f(x)=x+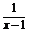 .
.
(2)证明 在曲线上任取一点(x0,x0+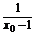 ),
),
由f′(x0)=1-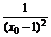 知,过此点的切线方程为
知,过此点的切线方程为
y-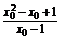 =
=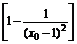 (x-x0).
(x-x0).
令x=1,得y=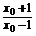 ,
,
切线与直线x=1的交点为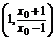 ;
;
令y=x,得y=2x0-1,
切线与直线y=x的交点为(2x0-1,2x0-1);
直线x=1与直线y=x的交点为(1,1),
从而所围三角形的面积为
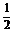
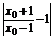 |2x0-1-1|=
|2x0-1-1|=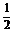
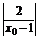 |2x0-2|=2.
|2x0-2|=2.
所以,所围三角形的面积为定值2.
10.求曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离.
解 设曲线上过点P(x0,y0)的切线平行于直线2x-y+3=0,即斜率是2,则y′|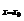 =
=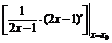
=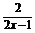 |
|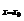 =
=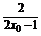 =2.
=2.
解得x0=1,所以y0=0,即点P(1,0),
点P到直线2x-y+3=0的距离为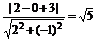 ,
,
∴曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是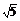 .
.
9.求下列函数在x=x0处的导数.
(1)f(x)=cosx·sin2x+cos3x,x0=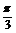 ;
;
(2)f(x)=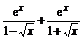 ,x0=2;
,x0=2;
(3)f(x)=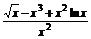 ,x0=1.
,x0=1.
解 (1)∵f′(x)=[cosx(sin2x+cos2x)]′
=(cosx)′=-sinx,
∴f′(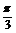 )=-
)=-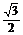 .
.
(2)∵f′(x)=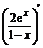
=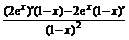
=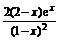 ,∴f′(2)=0.
,∴f′(2)=0.
(3)∵f′(x)=(x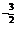 )′-x′+(lnx)′=-
)′-x′+(lnx)′=-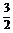 x
x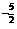 -1+
-1+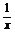 ,
,
∴f′(1)=- 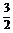 .
.
8.若函数f(x)的导函数为f′(x)=-x(x+1),则函数g(x)=f(logax)(0<a<1)的单调递减区间是 .
答案 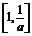
7.曲线y=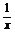 和y=x2在它们交点处的两条切线与x轴所围成的三角形面积是
.
和y=x2在它们交点处的两条切线与x轴所围成的三角形面积是
.
答案 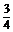
6.已知曲线S:y=3x-x3及点P(2,2),则过点P可向S引切线,其切线共有 条.
答案 3
5.(2009·徐州六县一区联考)若曲线f(x)=x4-x在点P处的切线平行于直线3x-y=0,则点P的坐标为 .
答案 (1,0)
4.曲线y=x3-2x2-4x+2在点(1,-3)处的切线方程是 .
答案 5x+y-2=0
3.若点P在曲线y=x3-3x2+(3-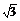 )x+
)x+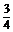 上移动,经过点P的切线的倾斜角为
上移动,经过点P的切线的倾斜角为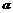 ,则角
,则角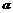 的取值范围是
.
的取值范围是
.
答案 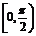
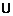
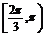
2.(2008·全国Ⅰ理,7)设曲线y=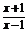 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=
.
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=
.
答案 -2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com