
3、函数的奇、偶性类型:
(1)奇函数:如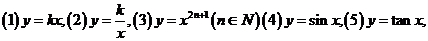
(2)偶函数:如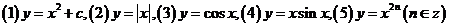
(3)非奇非偶函数:如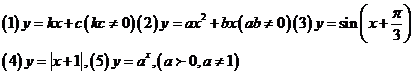
(4)既是奇函数又是偶函数:仅有一类:在定义域关于原点的对称区间上恒有f(x)=0.
2、奇、偶函数的性质:(1)奇函数的图象关于原点对称,偶函数的图象关于y轴对称。(2)奇函数在关于原点的对称区间上的单调性相同,偶函数在关于原点的对称区间上的单调性相反。
(3)若奇函数有对称轴x=a,则它有周期T=4a,偶函数有对称轴x=a,则它有周期T=2a,
(4)若奇函数在x=0处有定义则f(0)=0
1、函数的奇偶性定义:对于函数f(x)的定义域内的每一个值x,都有f(-x)=f(x),那么称f(x)为偶函数,如果对每一个值x都有f(-x)=-f(x),则称f(x)为奇函数。
3、常见函数的单调性:
(1) 一次函数y=kx+b(k≠0) 1)当k>0时,f(x)在R上是增函数。2)当k<0时,f(x)在R上是减函数。
(2)
二次函数y=ax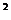 +bx+c 1)当a>o时,函数f(x)的图象开口向上,在(-∞,-
+bx+c 1)当a>o时,函数f(x)的图象开口向上,在(-∞,-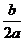 )上是减函数,在[-
)上是减函数,在[-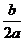 ,+∞)上是增函数,2) 当a<0时,函数f(x)的图象开口向下,在(-∞,-
,+∞)上是增函数,2) 当a<0时,函数f(x)的图象开口向下,在(-∞,-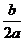 )上是增函数,在[-
)上是增函数,在[-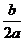 ,+∞)是减函数。
,+∞)是减函数。
(3)
反比例函数y=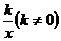 1) 当k>0时,f(x)在(-∞,0)与(0,+∞)上都是减函数,2) 当k<0时,f(x)在(-∞,0)与(0,+∞)上都是增函数但要注意在(-∞,0)∪(0,+∞)上f(x)没有单调性。
1) 当k>0时,f(x)在(-∞,0)与(0,+∞)上都是减函数,2) 当k<0时,f(x)在(-∞,0)与(0,+∞)上都是增函数但要注意在(-∞,0)∪(0,+∞)上f(x)没有单调性。
(4)
对钩函数: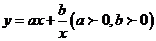 ,增区间为
,增区间为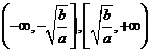 ,
,
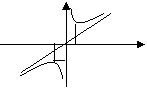
 减区间为
减区间为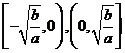 图象如右:
图象如右:

可采用导数法判断。
(5)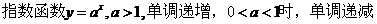
(6)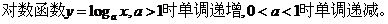
(7)三角函数:
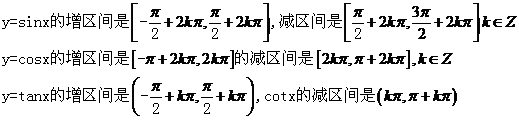
2、函数单调性的证明方法:通常根据定义,其步骤是:1)任取x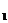 ,x
,x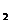 ∈D,且x
∈D,且x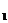 <x
<x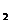 2)作差f(x
2)作差f(x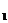 )- f(x
)- f(x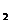 )或作商
)或作商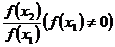 ,并变形,(4)判定f(x
,并变形,(4)判定f(x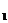 )- f(x
)- f(x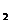 )的符号,或比较
)的符号,或比较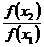 与1的大小, 4)根据定义作出结论。
与1的大小, 4)根据定义作出结论。
有时也根据导数。 (注:逆命题不成立)
(注:逆命题不成立)
1、定义:对于给定区间D上的函数f(x),若对于任意x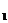 ,x
,x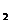 ∈D,当x
∈D,当x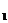 <x
<x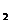 时,都有f(x
时,都有f(x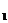 ) <f(x
) <f(x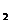 ),则称f(x)是区间上的增函数,当x
),则称f(x)是区间上的增函数,当x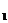 <x
<x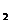 时,都有f(x
时,都有f(x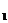 )> f(x
)> f(x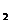 ),则称f(x)是区间上的减函数。如果函数y=
f(x)在区间上是增函数或减函数,就说函数y= f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。
),则称f(x)是区间上的减函数。如果函数y=
f(x)在区间上是增函数或减函数,就说函数y= f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。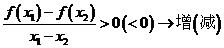 任意x
任意x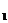 ,x
,x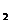 ∈D
∈D
1、求函数定义域的常用方法有:(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等。(2)根据实际问题的要求确定自变量的范围。(3)根据相关解析式的定义域来确定所求函数自变量的范围。(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x) 的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足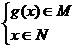 的x的集合。设y=f[g(x)]的定义域为P,则P
的x的集合。设y=f[g(x)]的定义域为P,则P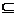 N。
N。
第三讲函数的单调性、周期性、奇偶性、反函数
5、构成函数的三要素:定义域,值域,对应法则。值域可由定义域唯一确定,因此当两个函数的定义域和对应法则相同时,值域一定相同,它们可以视为同一函数。
4、函数:(1)定义(传统):如果在某变化过程中有两个变量x,y并且对于x在某个范围内的每一个确定的值,按照某个对应法则,y都有唯一确定的值和它对应,那么y就是x的函数,x叫做自变量,x的取值范围叫做函数的定义域,和x的值对应的y的值叫做函数值,函数值的集合叫做函数的值域。(2)函数的集合定义:设A,B都是非空的数的集合,f:x→y是从A到B的映射,那么,从A到B的f:A→B,叫做A到B的函数,y=f(x),其中x∈A,y∈B,原像集合A叫做函数f(x)的定义域,像集合C叫做函数f(x)的值域。像集合C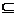 B
B
3、映射f:A→B的特征:(1)存在性:集合A中任一元素在集合B中都有像,(2)惟一性:集合A中的任一元素在集合B中的像只有一个,(3)方向性:从A到B的映射与从B到A的映射一般是不一样的(4)集合B中的元素在集合A中不一定有原象,若集合B中元素在集合A中有原像,原像不一定惟一。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com