
10. 解(1) 因为四边形ABCD是平行四边形, 所以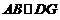 ········· 1分
········· 1分
所以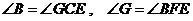
所以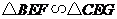 ·························· 3分
·························· 3分
(2)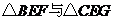 的周长之和为定值.················· 4分
的周长之和为定值.················· 4分
理由一:
过点C作FG的平行线交直线AB于H ,
因为GF⊥AB,所以四边形FHCG为矩形.所以 FH=CG,FG=CH
因此, 的周长之和等于BC+CH+BH
的周长之和等于BC+CH+BH
由 BC=10,AB=5,AM=4,可得CH=8,BH=6,
所以BC+CH+BH=24 ··························· 6分
理由二:
 由AB=5,AM=4,可知
由AB=5,AM=4,可知
在Rt△BEF与Rt△GCE中,有:
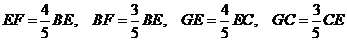 ,
,
所以,△BEF的周长是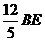 ,
△ECG的周长是
,
△ECG的周长是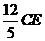
又BE+CE=10,因此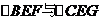 的周长之和是24. 6分
的周长之和是24. 6分
(3)设BE=x,则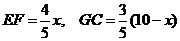
所以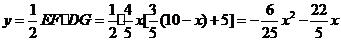 8分
8分
配方得: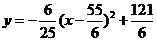 .
.
所以,当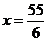 时,y有最大值. 9分
时,y有最大值. 9分
最大值为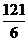 .
.
9. 解:(1)如图所示,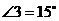 ,
,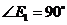 ,
,
∴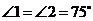 . ………………………………1分
. ………………………………1分
又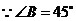 ,
,
∴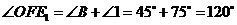 . ………3分
. ………3分
(2)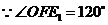 ,∴∠D1FO=60°.
,∴∠D1FO=60°.
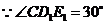 ,∴
,∴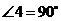 . ··················· 4分
. ··················· 4分
又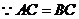 ,
,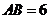 ,∴
,∴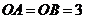 .
.
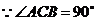 ,∴
,∴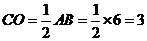 .··············· 5分
.··············· 5分
又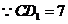 ,∴
,∴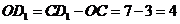 .
.
在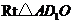 中,
中,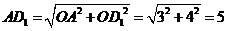 .········· 6分
.········· 6分
(3)点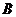 在
在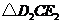 内部. ····················· 7分
内部. ····················· 7分
理由如下:设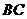 (或延长线)交
(或延长线)交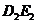 于点P,则
于点P,则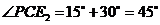 .
.
在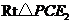 中,
中,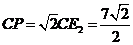 , …………········· 9分
, …………········· 9分
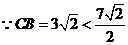 ,即
,即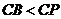 ,∴点
,∴点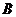 在
在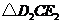 内部. ……………10分
内部. ……………10分
8.
(1)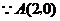 ,
,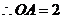 .
.
作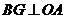 于
于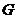 ,
,
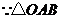 为正三角形,
为正三角形,
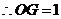 ,
,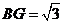 .
.
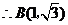 .
.
连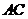 ,
,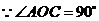 ,
,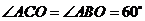 ,
,
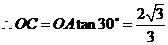 .
.

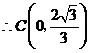 .
.
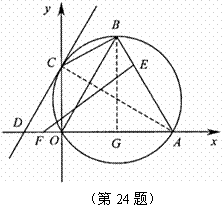
(2)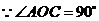 ,
,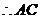 是圆的直径,
是圆的直径,
又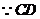 是圆的切线,
是圆的切线,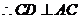 .
.
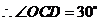 ,
,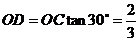 .
.
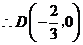 .
.
设直线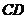 的函数解析式为
的函数解析式为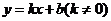 ,
,
则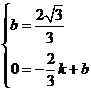 ,解得
,解得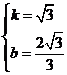 .
.
 直线
直线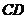 的函数解析式为
的函数解析式为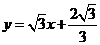 .
.
(3)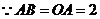 ,
,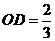 ,
,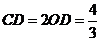 ,
,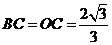 ,
,
 四边形
四边形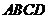 的周长
的周长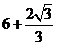 .
.
设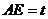 ,
,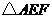 的面积为
的面积为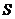 ,
,
则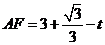 ,
,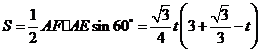 .
.
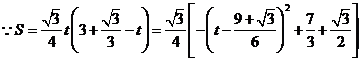 .
.
 当
当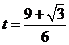 时,
时,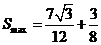 .
.
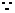 点
点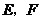 分别在线段
分别在线段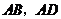 上,
上,
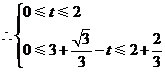 ,解得
,解得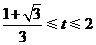 .
.
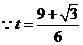 满足
满足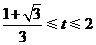 ,
,
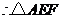 的最大面积为
的最大面积为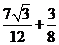 .
.
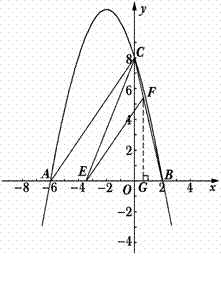
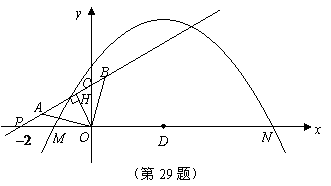
7. 解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
∴A、B、C三点的坐标分别是A(-6,0)、B(2,0)、C(0,8)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式y=ax2+bx+8,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)∵AB=8,OC=8
∴S△ABC =×8×8=32
(4)依题意,AE=m,则BE=8-m,
 ∵OA=6,OC=8, ∴AC=10
∵OA=6,OC=8, ∴AC=10
∵EF∥AC ∴△BEF∽△BAC
∴= 即= ∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
 ∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(5)存在. 理由:
∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.

6. [解] (1)若二分队在营地不休息,则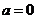 ,速度为4千米/时,行至塌方处需
,速度为4千米/时,行至塌方处需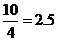 (小时),因为一分队到塌方处并打通道路需要
(小时),因为一分队到塌方处并打通道路需要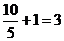 (小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到
(小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到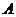 镇需
镇需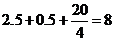 (小时).
(小时).
(2)一分队赶到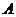 镇共需
镇共需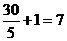 (小时).
(小时).
(ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故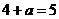 ,则
,则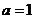 ,这与二分队在塌方处停留矛盾,舍去;
,这与二分队在塌方处停留矛盾,舍去;
(ⅱ)若二分队在塌方处不停留,则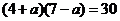 ,即
,即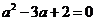 ,解得
,解得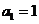 ,
,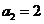 .
.
经检验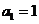 ,
,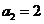 均符合题意.
均符合题意.
答:二分队应在营地休息1小时或2小时.
(3)合理的图象为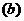 ,
,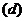 . 图象
. 图象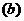 表明二分队在营地休息时间过长
表明二分队在营地休息时间过长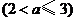 ,后于一分队赶到
,后于一分队赶到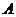 镇;图象
镇;图象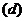 表明二分队在营地休息时间恰当
表明二分队在营地休息时间恰当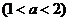 ,先于一分队赶到
,先于一分队赶到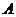 镇.
镇.
5. 解:(1)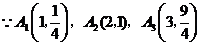
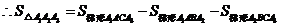
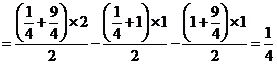
(2)①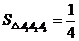 ,②
,②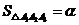 。
。
(3)由规律知: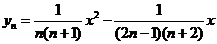 或写成(
或写成(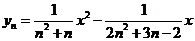 )
)
由(1)(2)知: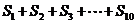
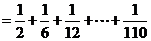
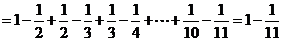
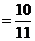
(4)存在.
由上知: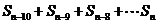
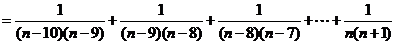
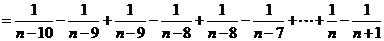
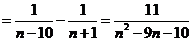
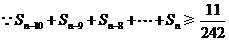 ,
,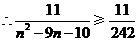
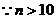 ,
,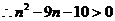 ,
,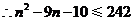 ,解得
,解得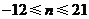
又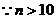 ,
,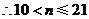 ,
, 存在
存在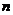 的最大值,其值为
的最大值,其值为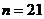 。
。
4. 解:(1)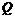 (1,0),点P运动速度每秒钟1个单位长度.
(1,0),点P运动速度每秒钟1个单位长度.
(2) 过点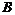 作BF⊥y轴于点
作BF⊥y轴于点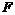 ,
,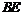 ⊥
⊥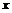 轴于点
轴于点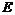 ,则
,则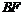 =8,
=8,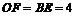 .
.
∴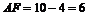 .在Rt△AFB中,
.在Rt△AFB中,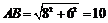 .
.
过点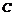 作
作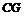 ⊥
⊥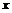 轴于点
轴于点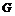 ,与
,与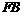 的延长线交于点
的延长线交于点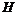 .
.
∵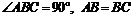 ∴△ABF≌△BCH.
∴
∴△ABF≌△BCH.
∴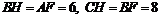 .
.
∴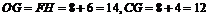 .∴所求C点的坐标为(14,12).
.∴所求C点的坐标为(14,12).
(3) 过点P作PM⊥y轴于点M,PN⊥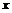 轴于点N,
轴于点N,
则△APM∽△ABF.,∴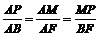 .,
.,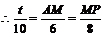 .
.
∴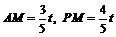 ,∴
,∴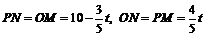 .
.
设△OPQ的面积为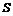 (平方单位),∴
(平方单位),∴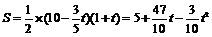 (0≤
(0≤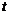 ≤10)
≤10)
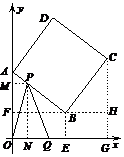 ∵
∵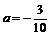 <0 ∴当
<0 ∴当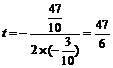 时, △OPQ的面积最大.,此时P的坐标为(
时, △OPQ的面积最大.,此时P的坐标为(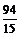 ,
,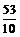 ) .
) .
(4)
当 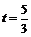 或
或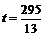 时, OP与PQ相等.
时, OP与PQ相等.
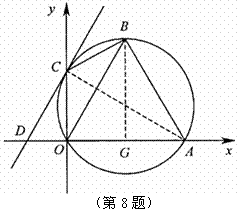
3.
[解] (1)由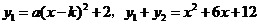
得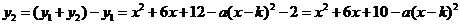 .
.
又因为当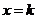 时,
时,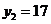 ,即
,即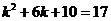 ,
,
解得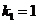 ,或
,或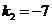 (舍去),故
(舍去),故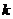 的值为
的值为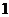 .
.
(2)由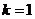 ,得
,得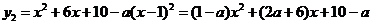 ,
,
所以函数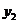 的图象的对称轴为
的图象的对称轴为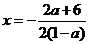 ,
,
于是,有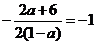 ,解得
,解得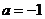 ,
,
所以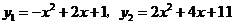 .
.
(3)由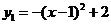 ,得函数
,得函数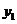 的图象为抛物线,其开口向下,顶点坐标为
的图象为抛物线,其开口向下,顶点坐标为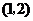 ;
;
由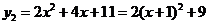 ,得函数
,得函数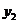 的图象为抛物线,其开口向上,顶点坐标为
的图象为抛物线,其开口向上,顶点坐标为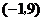 ;
;
故在同一直角坐标系内,函数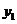 的图象与
的图象与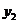 的图象没有交点.
的图象没有交点.
2. 解:(1)如图所示:··························· 4分

(注:正确画出1个图得2分,无作图痕迹或痕迹不正确不得分)
(2)若三角形为锐角三角形,则其最小覆盖圆为其外接圆;··········· 6分
若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆. 8分
 (3)此中转站应建在
(3)此中转站应建在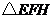 的外接圆圆心处(线段
的外接圆圆心处(线段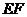 的垂直平分线与线段
的垂直平分线与线段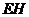 的垂直平分线的交点处). 10分
的垂直平分线的交点处). 10分
理由如下:
由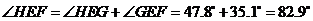 ,
,
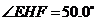 ,
,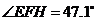 ,
,
故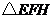 是锐角三角形,
是锐角三角形,
所以其最小覆盖圆为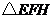 的外接圆,
的外接圆,
设此外接圆为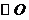 ,直线
,直线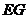 与
与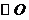 交于点
交于点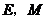 ,
,
则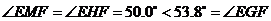 .
.
故点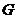 在
在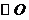 内,从而
内,从而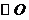 也是四边形
也是四边形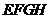 的最小覆盖圆.
的最小覆盖圆.
所以中转站建在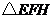 的外接圆圆心处,能够符合题中要求.
的外接圆圆心处,能够符合题中要求.
························· 12分
1. 解:(1)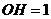 ;
;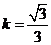 ,
,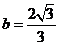 .
.
(2)设存在实数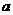 ,使抛物线
,使抛物线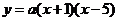 上有一点
上有一点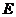 ,满足以
,满足以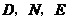 为顶点的三角形与等腰直角
为顶点的三角形与等腰直角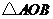 相似.
相似.
 以
以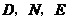 为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以
为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以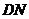 为直角边的等腰直角三角形,另一类是以
为直角边的等腰直角三角形,另一类是以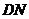 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.
①若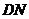 为等腰直角三角形的直角边,则
为等腰直角三角形的直角边,则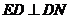 .
.
由抛物线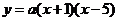 得:
得: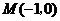 ,
,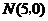 .
.
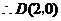 ,
,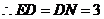 .
.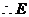 的坐标为
的坐标为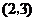 .
.
 把
把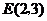 代入抛物线解析式,得
代入抛物线解析式,得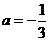 .
.
 抛物线解析式为
抛物线解析式为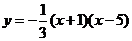 .
.
即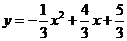 .
.
②若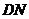 为等腰直角三角形的斜边,
为等腰直角三角形的斜边,
则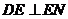 ,
,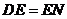 .
.
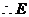 的坐标为
的坐标为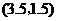 .
.
把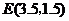 代入抛物线解析式,得
代入抛物线解析式,得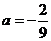 .
.
 抛物线解析式为
抛物线解析式为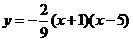 ,即
,即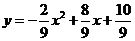
当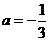 时,在抛物线
时,在抛物线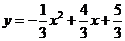 上存在一点
上存在一点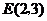 满足条件,如果此抛物线上还有满足条件的
满足条件,如果此抛物线上还有满足条件的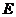 点,不妨设为
点,不妨设为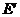 点,那么只有可能
点,那么只有可能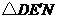 是以
是以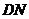 为斜边的等腰直角三角形,由此得
为斜边的等腰直角三角形,由此得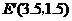 ,显然
,显然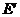 不在抛物线
不在抛物线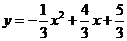 上,因此抛物线
上,因此抛物线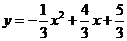 上没有符合条件的其他的
上没有符合条件的其他的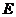 点.
点.
当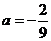 时,同理可得抛物线
时,同理可得抛物线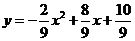 上没有符合条件的其他的
上没有符合条件的其他的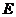 点.
点.
当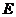 的坐标为
的坐标为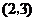 ,对应的抛物线解析式为
,对应的抛物线解析式为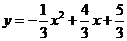 时,
时,
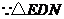 和
和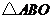 都是等腰直角三角形,
都是等腰直角三角形,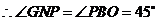 .
.
又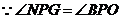 ,
,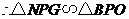 .
.
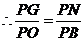 ,
,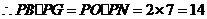 ,
, 总满足
总满足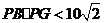 .
.
当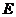 的坐标为
的坐标为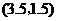 ,对应的抛物线解析式为
,对应的抛物线解析式为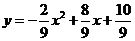 时,
时,
同理可证得: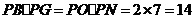 ,
, 总满足
总满足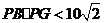
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com