36.(肥西中学高三物理第二次月考试卷)如图所示，质量均为m的物块A和B用弹簧连结起来，将它们悬于空中静止，弹簧处于原长状态，A距地面高度H=0.90m，同时释放两物块，A与地面碰撞后速度立即变为零，由于B的反弹，A刚好能离开地面。若B物块换为质量为2m的物块C(图中未画出)，仍将它们悬于空中静止且弹簧为原长，从A距地面高度为H’处同时释放，设A也刚好能离开地面。已知弹簧的弹性势能E_P与弹簧的劲度系数k和形变量x的关系是：E_P=kx²。试求：(1)B反弹后，弹簧的最大伸长量。(2)H’的大小

答案：(1)A落地时，B的速度为

υ_B=　　　　　　　　　　　　　　　　①

设反弹后上升的最大高度为x，

A恰好离开地面时 kx=mg 　　　　　　　　②

由系统机械能守恒 　mυ_B²=mgx+kx² 　　③

由①②③联立得　 x=0.6m

(2)将B换成C后，A落地时，C的速度为　 υ_C=　

C反弹后上升到最高时A刚好离开地面，　　 故仍有 kx=mg

由系统机械能守恒

1/2·2mυ_c²=2mgx+kx²　　　　　　 解得：H’=0.75m

35.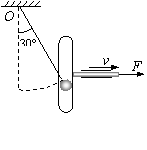(2009高淳外校月考)　 如图所示，轻且不可伸长的细绳悬挂质量为0．5kg 的小圆球，圆球又套在可沿水平方向移动的框架槽内，框架槽沿铅直方向，质量为0．2kg．自细绳静止于铅直位置开始，框架在水平力F=20N恒力作用下移至图中位置，此时细绳与竖直方向夹角30°．绳长0．2m，不计一切摩擦．

求：(1)此过程中重力对小圆球做功为多少？

(2)外力F做功为多大？

(3)小圆球在此位置的瞬时速度大小是多少．(取g=10m/s²)

答案(1)小球重力所做功为

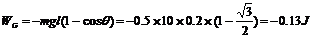
(2)外力F做功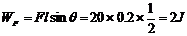　　　　

(3)将小球和框架槽看作一个系统，则系统动能定理：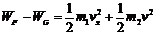

其中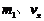为小球的质量和小球此时的速度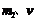，为框架槽的质量和此时的速度．

由运动的分解得：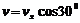　　　　　

代入上述方程：：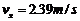　

34.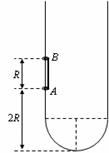(2009江浦中学月考)　 光滑的长轨道形状如图所示，底部为半圆型，半径R，固定在竖直平面内。AB两质量相同的小环用长为R的轻杆连接在一起，套在轨道上。将AB两环从图示位置静止释放，A环离开底部2R。不考虑轻杆和轨道的接触，即忽略系统机械能的损失，求：

(1)AB两环都未进入半圆型底部前，杆上的作用力。

(2)A环到达最低点时，两球速度大小。

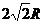(3)若将杆换成长　　　 ，A环仍从离开底部2R处静止释放，经过半圆型底部再次上升后离开底部的最大高度 。

答案⑴ 对整体自由落体，加速度为g； 以A为研究对象，A作自由落体则杆对A一定没有作用力。

⑵ AB都进入圆轨道后，两环具有相同角速度，则两环速度大小一定相等

整体机械能守恒：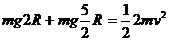　　

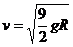
⑶　 A再次上升后，位置比原来高h，如图所示。

由动能定理　　 　　，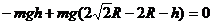　

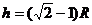A离开底部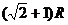

33.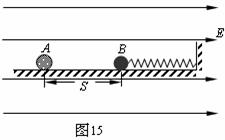(2009广东省茂名市模拟)　 如图15所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B，右端连在固定板上，放在光滑绝缘的水平面上。整个装置处在场强大小为E、方向水平向右的匀强电场中。现有一质量为m、带电荷量为+q的小球A，从距B球为S处自由释放，并与B球发生碰撞。碰撞中无机械能损失，且A球的电荷量始终不变。已知B球的质量M=3m，B球被碰后作周期性运动，其运动周期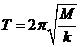(A、B小球均可视为质点)。

(1)求A球与B球第一次碰撞后瞬间，A球的速度V₁和B球的速度V₂；

(2)要使A球与B球第二次仍在B球的初始位置迎面相碰，求劲度系数k的可能取值。

答案：(1)设A球与B球碰撞前瞬间的速度为v₀，

由动能定理得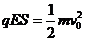，　　 　　　　　　　　①

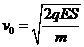解得：　　　　　 　　　　　　　　②

碰撞过程中动量守恒　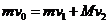　　　 　　　③

机械能无损失，有　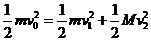　　　 　　④

解得　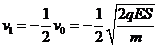 　　负号表示方向向左　

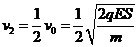　　　 方向向右　　　　　　　

(2)要使m与M第二次迎面碰撞仍发生在原位置，则必有A球重新回到O处所用　　　　 的时间t恰好等于B球的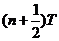

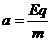　　 ⑥

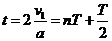(n=0 、1 、2 、3 ……)　 ⑦

由题意得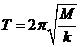： 　　　　　　　　　⑧

解得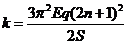：　 (n=0 、1 、2 、3 ……) ⑨

32.(2009南阳中学月考)　 如图所示，质量m=60kg的高山滑雪运动员，从A点由静止开始沿滑雪道滑下，从B点水平飞出后又落在与水平面成倾角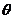=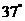的斜坡上C点．已知AB两点间的高度差为h=25m，B、C两点间的距离为s=75m，已知sin37⁰=0.6，取g=10m/s²，求：

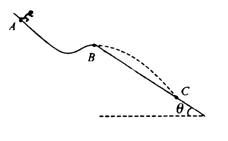
(1)运动员从B点水平飞出时的速度大小；

(2)运动员从A点到B点的过程中克服摩擦力做的功．

解：(1)由B到C平抛运动的时间为t

竖直方向：h_Bc=ssin37^o=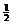gt²　　　　 (1)　　　

水平方向：scos37⁰=v_Bt 　　　　　　　(2)　

代得数据，解(1)(2)得v_B=20m／s　 (3)　

(2)A到B过程，由动能定理有

mgh_AB+w_f=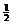mv_B² 　　　　　　　　　(4)　

代人数据，解(3)(4)得　 w_f ＝－3000J　　

所以运动员克服摩擦力所做的功为3000J

31.(2009东城区期末试题)　 如图所示，在距水平地面高h＝0.80m的水平桌面一端的边缘放置一个质量m＝0.80kg的木块B，桌面的另一端有一块质量M=1.0kg的木块A以初速度v₀=4.0m/s开始向着木块B滑动，经过时间t=0.80s与B发生碰撞，碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点，它们的碰撞时间极短，且已知D点距桌面边缘的水平距离s=0.60m，木块A与桌面间的动摩擦因数μ=0.25，重力加速度取g＝10m/s²。求：

(1)两木块碰撞前瞬间，木块A的速度大小；

(2)木块B离开桌面时的速度大小；

(3)木块A落到地面上的位置与D点之间的距离。

答案：(1)木块A在桌面上受到滑动摩擦力作用做匀减速运动，根据牛顿第二定律，木块A的加速度　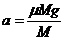　 ＝2.5m/s²

设两木块碰撞前A的速度大小为v，根据运动学公式，得

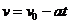＝2.0m/s…

(2)两木块离开桌面后均做平抛运动，设木块B离开桌面时的速度大小为v₂，在空中飞行的时间为t′。根据平抛运动规律有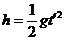：，s＝v₂t′

解得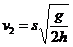：　　　　　　　　　　 ＝1.5m/s

(3)设两木块碰撞后木块A的速度大小为v₁，根据动量守恒定律有：

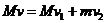
解得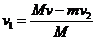：　　　　　　　　　　　 =0.80m/s

设木块A落到地面过程的水平位移为s′，根据平抛运动规律，得

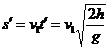　　　　　　　　　　 ＝0.32m

则木块A落到地面上的位置与D点之间的距离　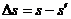 ＝0.28m

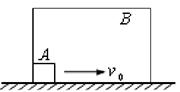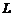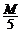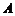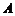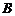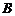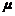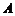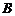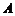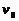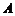30.(2009年广东省实验中学模拟)如图所示，矩形盒的质量为，底部长度为，放在水平面上，盒内有一质量为可视为质点的物体，与、与地面的动摩擦因数均为，开始时二者均静止，在的左端。现瞬间使物体获得一向右的水平初速度，以后物体与盒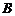的左右壁碰撞时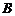，始终向右运动。当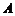与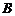的左壁最后一次碰撞后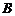，立刻停止运动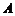，继续向右滑行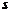(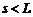)后也停止运动。

(1)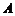与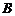第一次碰撞前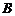，是否运动？

(2)若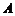第一次与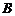碰后瞬间向左运动的速率为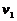，求此时矩形盒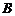的速度大小

(3)当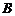停止运动时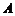，的速度是多少？

答案　 (1) 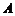与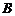第一次碰撞前，A、B之间的压力等于A的重力，即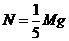

A对B的摩擦力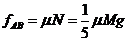

而B与地面间的压力等于A、B重力之和，即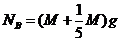

地面对B的最大静摩擦力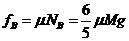

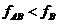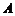　　　 故与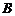第一次碰撞前，B不运动

(2)设A第一次碰前速度为v，碰后B的速度为v₂

则由动能定理有

…

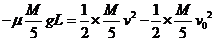碰撞过程中动量守恒

有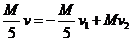　　　　

解得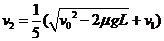

(3)当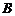停止运动时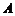， 继续向右滑行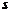(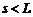)后停止，设B停止时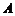，的速度为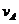，则由动能定理…

得…

解得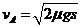

29.(2009年深圳一模)　 光滑水平面上有两个小木块A和B，其质量m_A=1kg、m_B=4kg，它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g，以V₀=500m/s的速度在极短时间内射穿两木块，已知射穿A木块后子弹的速度变为原来的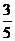，且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍.求:系统运动过程中弹簧的最大弹性势能.

答案　 弹穿过A时，子弹与A动量守恒，

由动量守恒定律： ………………………　 ①　

而由　 得：v1=300m/s

得：　 ………………………②

子弹穿过B时， 子弹与B动量守恒，

由动量守恒定律：　　 ………………………③

又由　 …………………④　

得：v2=100m/s

由③，④得：　 ………………………⑤

子弹穿过B以后，弹簧开始被压缩，A、B和弹簧所组成的系统动量守恒

由动量守恒定律：　 ………………………⑥　

由能量关系：　 ……………………⑦

由② ⑤ ⑥ ⑦得：　 ………………………⑧　

28.(合肥35中2009届高三10月月考物理试卷)质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P

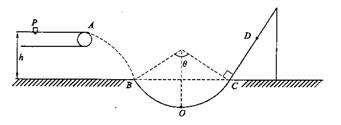　 　 　 点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点，其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角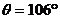，轨道最低点为O，A点距水平面的高度h=0.8m。小物块离开C点后恰能无碰撞的沿固定斜面向上运动，0.8s后经过D点，物块与斜面间的滑动摩擦因数为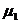=0.33(g=10m/s²,sin37°=0.6,cos37°=0.8)试求：

(1)小物块离开A点的水平初速度v₁　

(2)小物块经过O点时对轨道的压力　

(3)斜面上CD间的距离　

(4)假设小物块与传送带间的动摩擦因数为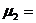0.3，传送带的速度为5m/s，则PA间的距离是多少？

答案：(1)对小物块，由A到B有：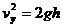　

在B点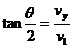　　 　　　 所以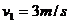

(2)对小物块，由B到O有：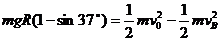　

其中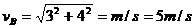　　

在O点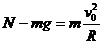　 　　　　 所以N=43N

由牛顿第三定律知对轨道的压力为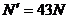

(3)物块沿斜面上滑：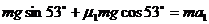

所以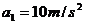

物块沿斜面上滑：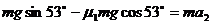　

由机械能守恒知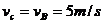

小物块由C上升到最高点历时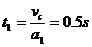

小物块由最高点回到D点历时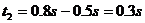

故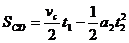　　

即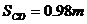　

(4)小物块在传送带上加速过程：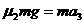

PA间的距离是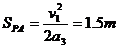　

27.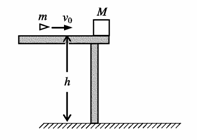(2009宣武区期末试题) 　如图，一质量为M =1.2kg的物块静止在桌面边缘，桌面离水平地面的高度为h =1.8m。一质量为m=20g的子弹以水平速度v₀=100m/s射入物块，在很短的时间内以水平速度10m/s穿出。重力加速度g取10m/s²。求：

(1)子弹穿出木块时，木块获得的水平初速度V；

(2)木块落地点离桌面边缘的水平距离X。

答案　 (1)　 ∵ mv₀=mv+MV 　　∴V=(mv₀-mv)/M =1.5m/s

(2)∵ h =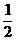gt²X=V·t　　

　∴ X=V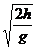=0.9m