
27. 解:(1)由题意知重叠部分是等腰直角三角形,作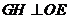 .
.
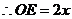 ,
,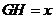 ,
,
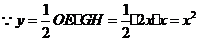 (
(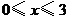 ) 5分
) 5分
(2)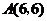 )
)
当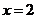 时,
时,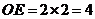 .
.
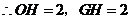 ,
,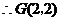 .
.
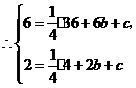
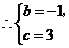
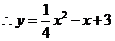 . 5分
. 5分
(3)设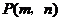 .
.
当点 到
到 轴的距离为
轴的距离为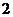 时,有
时,有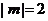 ,
,
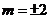 .
.
当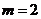 时,得
时,得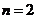 ,
,
当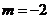 时,得
时,得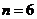 .
.
当点 到
到 轴的距离为2时,有
轴的距离为2时,有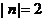 .
.
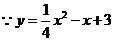
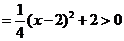
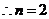 .
.
当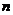
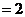 时,得
时,得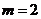 .
.
综上所述,符合条件的点 有两个,分别是
有两个,分别是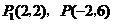 . 4分
. 4分
26. (1)解法一:设抛物线的解析式为y = a (x +3 )(x - 4)
因为B(0,4)在抛物线上,所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3
所以抛物线解析式为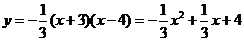
解法二:设抛物线的解析式为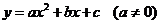 ,
,
依题意得:c=4且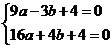 解得
解得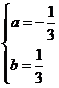
所以 所求的抛物线的解析式为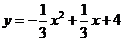
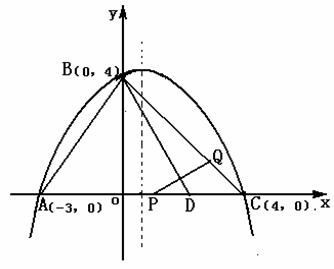
(2)连接DQ,在Rt△AOB中,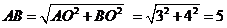
所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2
因为BD垂直平分PQ,所以PD=QD,PQ⊥BD,所以∠PDB=∠QDB
因为AD=AB,所以∠ABD=∠ADB,∠ABD=∠QDB,所以DQ∥AB
所以∠CQD=∠CBA。∠CDQ=∠CAB,所以△CDQ∽ △CAB
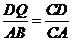 即
即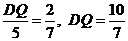
所以AP=AD – DP = AD – DQ=5 –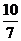 =
=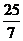 ,
,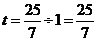
所以t的值是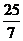
(3)答对称轴上存在一点M,使MQ+MC的值最小
理由:因为抛物线的对称轴为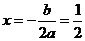
所以A(- 3,0),C(4,0)两点关于直线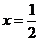 对称
对称
连接AQ交直线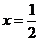 于点M,则MQ+MC的值最小
于点M,则MQ+MC的值最小
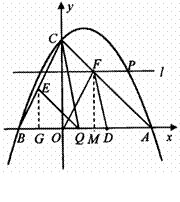
过点Q作QE⊥x轴,于E,所以∠QED=∠BOA=900
DQ∥AB,∠ BAO=∠QDE, △DQE ∽△ABO
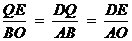 即
即 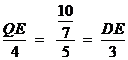
所以QE=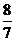 ,DE=
,DE=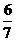 ,所以OE = OD + DE=2+
,所以OE = OD + DE=2+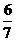 =
=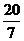 ,所以Q(
,所以Q(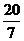 ,
,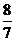 )
)
设直线AQ的解析式为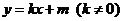
则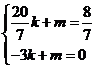 由此得
由此得 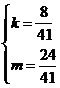
所以直线AQ的解析式为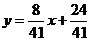 联立
联立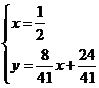
由此得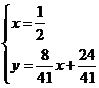 所以M
所以M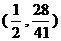
则:在对称轴上存在点M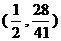 ,使MQ+MC的值最小。
,使MQ+MC的值最小。
3.图形大致画得正确的得2分.
3.第填对其中4空得1分;
2.第(2)问回答正确的得1分,证明正确的得1分,求出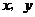 的值各得1分;
的值各得1分;
25. 解:(1)过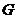 作
作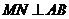 于
于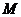 交
交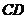 于
于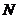 ,
,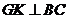 于
于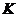 .
.
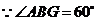 ,
,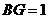 ,
,
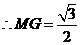 ,
,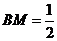 .
.
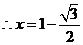 ,
,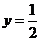 . 2分
. 2分
(2)当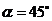 时,点
时,点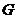 在对角线
在对角线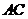 上,其理由是: 3分
上,其理由是: 3分
过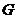 作
作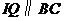 交
交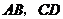 于
于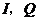 ,
,
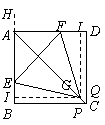 过
过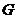 作
作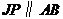 交
交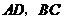 于
于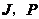 .
.
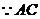 平分
平分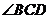 ,
,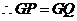 ,
,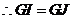 .
.
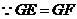 ,
,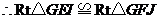 ,
,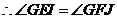 .
.
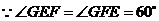 ,
,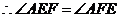 .
.
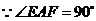 ,
,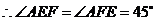 .
.
即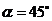 时,点
时,点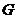 落在对角线
落在对角线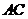 上. 4分
上. 4分
(以下给出两种求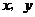 的解法)
的解法)
方法一: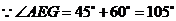 ,
,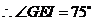 .
.
在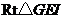 中,
中,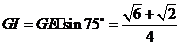 ,
,
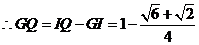 . 5分
. 5分
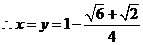 . 6分
. 6分
方法二:当点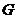 在对角线
在对角线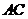 上时,有
上时,有
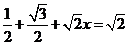 , 5分
, 5分
解得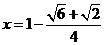
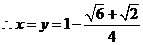 . 6分
. 6分
(3)
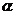 |
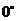 |
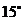 |
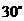 |
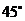 |
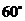 |
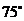 |
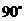 |
 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
0.29 |
0.50 |
 |
0.50 |
0.29 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
8分
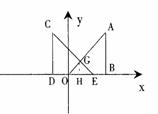
(4)由点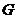 所得到的大致图形如图所示:
所得到的大致图形如图所示:

 10分
10分
说明:1.第(1)问中,写对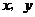 的值各得1分;
的值各得1分;
24. (1)连结OB、OC,由∠BAD=75°,OA=OB知∠AOB=30°,
∵AB=CD,∴∠COD=∠AOB=30°,∴∠BOC=120°,
故的长为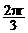 .
.
(2)连结BD,∵AB=CD,∴∠ADB=∠CBD,∴BC∥AD,
同理EF∥AD,从而BC∥AD∥FE.
(3)过点B作BM⊥AD于M,由(2)知四边形ABCD为等腰梯形,从而BC=AD-2AM=2r-2AM.
∵AD为直径,∴∠ABD=90°,易得△BAM∽△DAB
∴AM=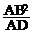 =
=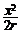 ,∴BC=2r-
,∴BC=2r-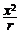 ,同理EF=2r-
,同理EF=2r-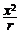
∴L=4x+2(2r-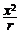 )=
)=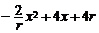 =
=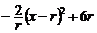 ,其中0<x<
,其中0<x<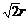
∴当x=r时,L取得最大值6r.
23.
解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA
∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°
∴∠BAE=∠CDA
又∠B=∠C=45°
∴∆ABE∽∆DCA
(2)∵∆ABE∽∆DCA
∴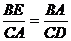
由依题意可知CA=BA=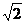
∴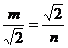
∴m=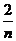
自变量n的取值范围为1<n<2.
(3)由BD=CE可得BE=CD,即m=n
∵m=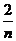
∴m=n=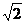
∵OB=OC=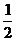 BC=1
BC=1
∴OE=OD=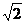 -1
-1
∴D(1-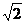 , 0)
, 0)
∴BD=OB-OD=1-(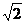 -1)=2-
-1)=2-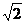 =CE,
DE=BC-2BD=2-2(2-
=CE,
DE=BC-2BD=2-2(2-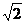 )=2
)=2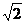 -2
-2
∵BD +CE
+CE =2 BD
=2 BD =2(2-
=2(2-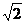 )
) =12-8
=12-8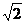 , DE
, DE =(2
=(2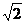 -2)
-2) = 12-8
= 12-8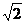
∴BD +CE
+CE =DE
=DE
(4)成立
证明:如图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,则CE=HB,AE=AH,
∠ABH=∠C=45°,旋转角∠EAH=90°.
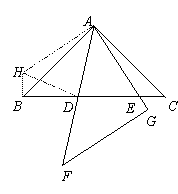
连接HD,在∆EAD和∆HAD中
∵AE=AH, ∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD.
∴∆EAD≌∆HAD
∴DH=DE
又∠HBD=∠ABH+∠ABD=90°
∴BD +HB
+HB =DH
=DH
即BD +CE
+CE =DE
=DE
22. 解:(1)由抛物线过B(0,1) 得c=1.
又b=-4ac,
顶点A(-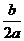 ,0),
,0),
∴-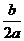 =
=
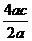 =2c=2.∴A(2,0).
=2c=2.∴A(2,0).
将A点坐标代入抛物线解析式,得4a+2b+1=0 ,
∴ 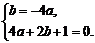 解得a =
解得a =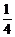 ,b =-1.
,b =-1.
故抛物线的解析式为y=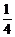 x2-x+1.
x2-x+1.
 另解: 由抛物线过B(0,1)
得c=1.又b2-4ac=0,
b=-4ac,∴b=-1.
另解: 由抛物线过B(0,1)
得c=1.又b2-4ac=0,
b=-4ac,∴b=-1.
∴a=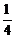 ,故y=
,故y=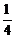 x
x -x+1.
-x+1.
(2)假设符合题意的点C存在,其坐标为C(x,y),
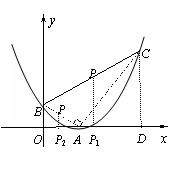 作CD⊥x轴于D ,连接AB、AC.
作CD⊥x轴于D ,连接AB、AC.
∵A在以BC为直径的圆上,∴∠BAC=90°.
∴ △AOB∽△CDA.
∴OB·CD=OA·AD.
即1·y=2(x-2), ∴y=2x-4.
由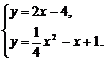
解得x1=10,x2=2.
∴符合题意的点C存在,且坐标为 (10,16),或(2,0).
∵P为圆心,∴P为BC中点.
当点C坐标为 (10,16)时,取OD中点P1 ,连PP1 , 则PP1为梯形OBCD中位线.
∴PP1=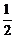 (OB+CD)=
(OB+CD)=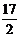 .∵D (10,0), ∴P1 (5,0), ∴P (5,
.∵D (10,0), ∴P1 (5,0), ∴P (5, 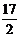 ).
).
当点C坐标为 (2,0)时, 取OA中点P2 ,连PP2 , 则PP2为△OAB的中位线.
∴PP2=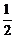 OB=
OB= .∵A (2,0), ∴P2(1,0), ∴P
(1,
.∵A (2,0), ∴P2(1,0), ∴P
(1, ).
).
故点P坐标为(5, 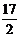 ),或(1,
),或(1, ).
).
(3)设B、P、C三点的坐标为B(x1,y1), P(x2,y2), C(x3,y3),由(2)可知:
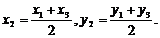
21.解:(1)由题意,得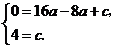 )
)
解得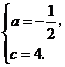
 所求抛物线的解析式为:
所求抛物线的解析式为: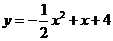 .
.
(2)设点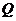 的坐标为
的坐标为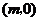 ,过点
,过点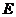 作
作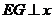 轴于点
轴于点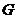 .
.
由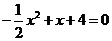 ,得
,得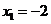 ,
,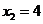 .
.
 点
点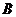 的坐标为
的坐标为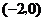 .
.
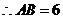 ,
,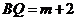 .
.
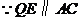 ,
,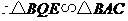 .
.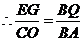 ,
,
即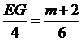 .
.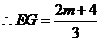 .
.
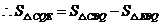
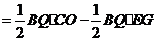
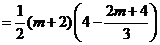
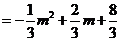
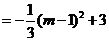 .
.
又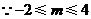 ,
,
 当
当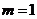 时,
时,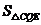 有最大值3,此时
有最大值3,此时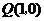 .
.
(3)存在.
在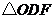 中.
中.
(ⅰ)若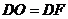 ,
,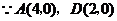 ,
,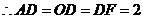 .
.
又在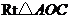 中,
中,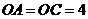 ,
,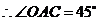 .
.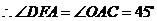 .
.
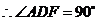 .此时,点
.此时,点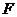 的坐标为
的坐标为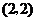 .
.
由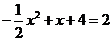 ,得
,得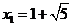 ,
,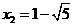 .
.
此时,点 的坐标为:
的坐标为: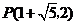 或
或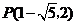 .
.
(ⅱ)若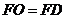 ,过点
,过点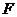 作
作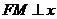 轴于点
轴于点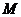 ,
,
由等腰三角形的性质得: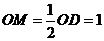 ,
,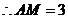 ,
,
 在等腰直角
在等腰直角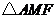 中,
中,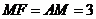 .
.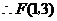 .
.
由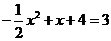 ,得
,得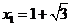 ,
,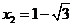 .
.
此时,点 的坐标为:
的坐标为: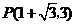 或
或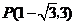 .
.
(ⅲ)若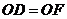 ,
,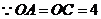 ,且
,且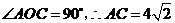 ,
,
 点
点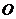 到
到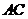 的距离为
的距离为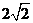 ,而
,而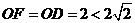 ,
,
此时,不存在这样的直线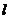 ,使得
,使得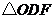 是等腰三角形.
是等腰三角形.
综上所述,存在这样的直线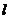 ,使得
,使得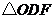 是等腰三角形.所求点
是等腰三角形.所求点 的坐标为:
的坐标为:
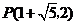 或
或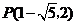 或
或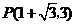 或
或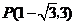
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com