
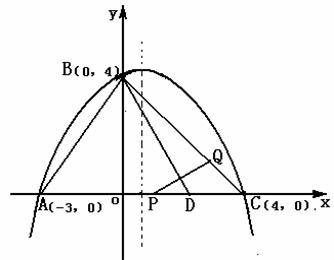
26.(08莆田市)如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1) 求抛物线的解析式.
(2)已知AD = AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由。
(注:抛物线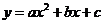 的对称轴为
的对称轴为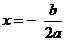 )
)
25.( 2008 江西)如图1,正方形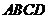 和正三角形
和正三角形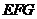 的边长都为1,点
的边长都为1,点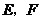 分别在线段
分别在线段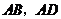 上滑动,设点
上滑动,设点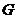 到
到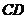 的距离为
的距离为 ,到
,到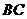 的距离为
的距离为 ,记
,记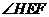 为
为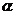 (当点
(当点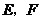 分别与
分别与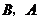 重合时,记
重合时,记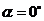 ).
).
(1)当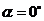 时(如图2所示),求
时(如图2所示),求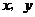 的值(结果保留根号);
的值(结果保留根号);
(2)当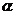 为何值时,点
为何值时,点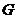 落在对角线
落在对角线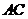 上?请说出你的理由,并求出此时
上?请说出你的理由,并求出此时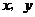 的值(结果保留根号);
的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
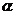 |
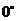 |
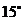 |
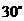 |
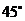 |
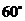 |
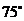 |
 |
 |
|
0.03 |
0 |
|
|
0.29 |
|
 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点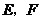 分别在线段
分别在线段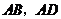 上滑动”改为“点
上滑动”改为“点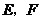 分别在正方形
分别在正方形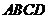 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点
边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点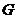 运动所形成的大致图形.
运动所形成的大致图形.
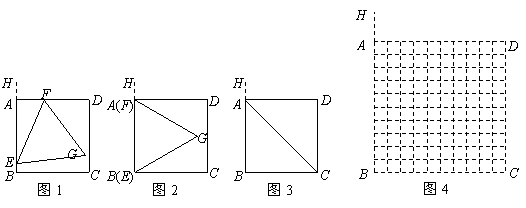 (参考数据:
(参考数据: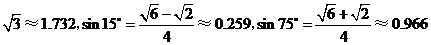 .)
.)
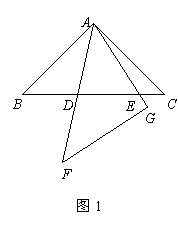
23.(2008 湖北 恩施) 如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
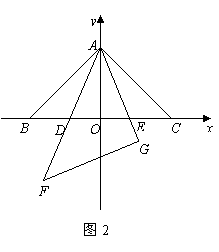
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD +CE
+CE =DE
=DE .
.
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE =DE
=DE 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.


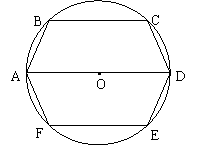
24. (2008 湖南 长沙)如图,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.
(1)当∠BAD=75°时,求的长;
(2)求证:BC∥AD∥FE;
 (3)设AB=
(3)设AB=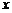 ,求六边形ABCDEF的周长L关于
,求六边形ABCDEF的周长L关于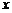 的函数关系式,并指出
的函数关系式,并指出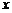 为何值时,L取得最大值.
为何值时,L取得最大值.
22.(2008 湖北 荆门)已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点为B(0,1),且b=-4ac.
(1) 求抛物线的解析式;
(2) 在抛物线上是否存在一点C,使以BC为直径的圆经过抛物线的顶点A?若不存在说明理由;若存在,求出点C的坐标,并求出此时圆的圆心点P的坐标;
(3) 根据(2)小题的结论,你发现B、P、C三点的横坐标之间、纵坐标之间分别有何关系?
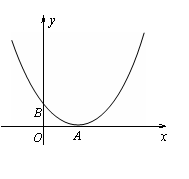

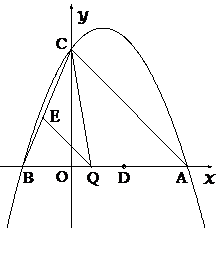
21. (2008 重庆)已知:如图,抛物线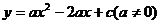 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ。当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线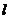 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。问:是否存在这样的直线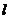 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。

20.(2008 湖南
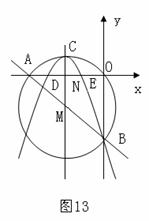
怀化)如图13,在平面直角坐标系中,圆M经过原点O,且与 轴、
轴、 轴分别相交于
轴分别相交于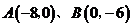 两点.
两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于 轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交 轴于D、E两点,在抛物线上是否存在点P,使得
轴于D、E两点,在抛物线上是否存在点P,使得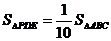 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
19.(2008 河北)如图,在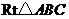 中,
中,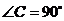 ,
,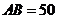 ,
,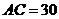 ,
,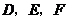 分别是
分别是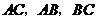 的中点.点
的中点.点 从点
从点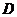 出发沿折线
出发沿折线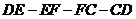 以每秒7个单位长的速度匀速运动;点
以每秒7个单位长的速度匀速运动;点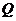 从点
从点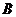 出发沿
出发沿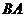 方向以每秒4个单位长的速度匀速运动,过点
方向以每秒4个单位长的速度匀速运动,过点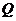 作射线
作射线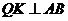 ,交折线
,交折线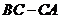 于点
于点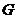 .点
.点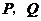 同时出发,当点
同时出发,当点 绕行一周回到点
绕行一周回到点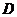 时停止运动,点
时停止运动,点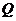 也随之停止.设点
也随之停止.设点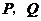 运动的时间是
运动的时间是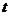 秒(
秒(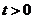 ).
).
(1)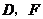 两点间的距离是 ;
两点间的距离是 ;
(2)射线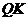 能否把四边形
能否把四边形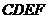 分成面积相等的两部分?若能,求出
分成面积相等的两部分?若能,求出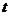 的值.若不能,说明理由;
的值.若不能,说明理由;
(3)当点 运动到折线
运动到折线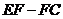 上,且点
上,且点 又恰好落在射线
又恰好落在射线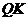 上时,求
上时,求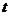 的值;
的值;
(4)连结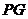 ,当
,当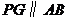 时,请直接写出
时,请直接写出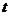 的值.
的值.


18. (2008四川广安)如图,已知抛物线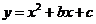 经过点(1,-5)和(-2,4)
经过点(1,-5)和(-2,4)
(1)求这条抛物线的解析式.
(2)设此抛物线与直线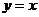 相交于点A,B(点B在点A的右侧),平行于
相交于点A,B(点B在点A的右侧),平行于 轴的直线
轴的直线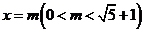 与抛物线交于点M,与直线
与抛物线交于点M,与直线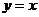 交于点N,交
交于点N,交 轴于点P,求线段MN的长(用含
轴于点P,求线段MN的长(用含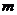 的代数式表示).
的代数式表示).
(3)在条件(2)的情况下,连接OM、BM,是否存在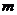 的值,使△BOM的面积S最大?若存在,请求出
的值,使△BOM的面积S最大?若存在,请求出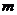 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
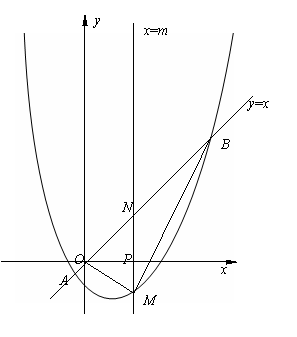

17.(2008湖北十堰)已知抛物线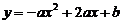 与
与 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
⑴直接写出抛物线的对称轴,及抛物线与 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;
⑶坐标平面内是否存在点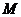 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点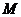 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
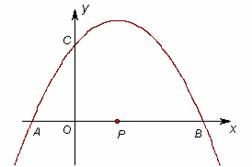
16.(2008 四川 泸州)如图11,已知二次函数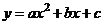 的图像经过三点A
的图像经过三点A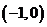 ,B
,B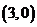 ,C
,C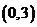 ,它的顶点为M,又正比例函数
,它的顶点为M,又正比例函数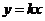 的图像于二次函数相交于两点D、E,且P是线段DE的中点。
的图像于二次函数相交于两点D、E,且P是线段DE的中点。
⑴求该二次函数的解析式,并求函数顶点M的坐标;
⑵已知点E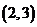 ,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量
,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量 的取值范围;
的取值范围;
⑶当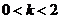 时,求四边形PCMB的面积
时,求四边形PCMB的面积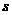 的最小值。
的最小值。

[参考公式:已知两点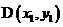 ,
,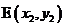 ,则线段DE的中点坐标为
,则线段DE的中点坐标为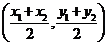 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com