2．如图6-24，在高出地平面50米的小山上有一塔AB，在地面D测得塔顶A和塔基B的仰面分别为50°和45°，求塔高．

1．某一时刻，太阳光线与地平面的夹角为78°，此时测得烟囱的影长为5米，求烟囱的高(精确到0.1米)．

(三)总结与扩展

请学生总结：通过学习两个例题，初步学会把一些实际问题转化为数学问题，通过解直角三角形来解决，具体说，本节课通过让学生把实际问题转化为数学问题，利用正切或余切解直角三角形，从而把问题解决．

本课涉及到一种重要教学思想：转化思想．

(二)重点、难点的学习与目标完成过程．

1．例1如图6-21，厂房屋顶人字架(等腰三角形)的跨度为10米，∠A-26°，求中柱BC(C为底边中点)和上弦AB的长(精确到0.01米)．

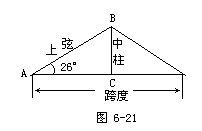
分析：上图是本题的示意图，同学们对照图形，根据题意思考题目中的每句话对应图中的哪个角或边，本题已知什么，求什么？

由题意知，△ABC为直角三角形，∠ACB=90°，∠A=26°，AC=5米，可利用解Rt△ABC的方法求出BC和AB．

学生在把实际问题转化为数学问题后，大部分学生可自行完成．

解：∵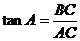

∴BC=AC·tanA=5×tan26°≈2.44(米)．

∵AB=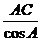==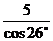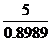≈5.56(米)

答：中柱BC约长2.44米，上弦AB约=长5.56米．

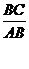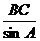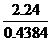例题小结：求出中柱BC的长为2.44米后，我们也可以利用正弦计算上弦AB的长，即由 sinA==得AB=≈≈5.75(米)。

这个结果与例1中所得的结果相比较，相差0.01米，这两个结果都可认为是正确的，因为cos26°、sin26°都取近似值，相除以后又取近似值，经过两次近似后，出现0.01米的差异，在本例中认为是可以的．

但是在求AB时，我们应尽量应用题目中原有的已知量，也就是选用关系式

　AB=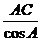=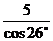求得结果。

如果在引导学生讨论后小结，效果会更好，不仅使学生掌握选何关系式，更重要的是知道为什么选这个关系式，以培养学生分析问题、解决问题的能力及计算能力，形成良好的学习习惯．

另外，本题是把解等腰三角形的问题转化为直角三角形的问题，渗透了转化的数学思想．

2．巩固练习

教材P．119练习．

引导学生根据示意图，说明本题已知什么，求什么，利用哪个三角形来求解，用正弦、余弦、正切、余切中的哪一种解较为简便？

3．补充例题2

为测量松树AB的高度，一个人站在距松树15米的E处，测得仰角∠ACD=52°，已知人的高度是1.72米，求树高(精确到0.01米)．

首先请学生结合题意画几何图形，并把实际问题转化为数学问题．

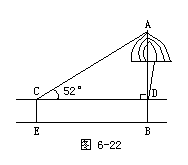
Rt△ACD中，∠D=Rt∠，∠ACD=52°，CD=BE=15米，CE=DB=1.72米，求AB？

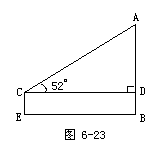
解：在RtΔACD中，tanC=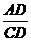

∴AD=CD·tanC=BE·tanC

=15×tan52°=15×1.2799

≈19.20(米)．

∴AB=AD+BD=19.20+1.72

=20.92(米)．

答：树高20.92米．

(一)明确目标

1．直角三角形中除直角外五个元素之间具有什么关系？请学生口答．

2．等腰三角形具有什么性质？

以上二题，通过提问学生，唤起学生的记忆，为本节课的学习奠定基础．

3．导入新课

上节课我们解决的实际问题是应用正弦及余弦解直角三角形，在实际问题中有时还经常应用正切和余切来解直角三角形，从而使问题得到解决．

3．疑点：计算例1时，选不同的三角函数所得结果却不相同，学生会感到疑惑．

2．难点：要求学生善于将某些实际问题中的数量关系，归结为直角三角形中元素之间的关系，从而利用所学知识把实际问题解决．

1．重点：要求学生善于将某些实际问题中的数量关系，归结为直角三角形元素之间的关系，从而利用所学知识把实际问题解决．

(三)德育渗透点

渗透数学来源于实践又反过来作用于实践的观点，培养学生用数学的意识．

(二)能力训练点

逐步培养学生分析问题、解决问题的能力．