
1.光在同一均匀介质中是沿直线传播的
前提条件是在同一均匀介质。否则,可能发生偏折。如光从空气斜射入水中(不是同一种介质);“海市蜃楼”现象(介质不均匀)。
2.若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为( )
A.18° B.36° C.72° D.144°
4.(1)AB=5>1+3,外离.
(2)设B(x,0)x≠-2,则AB=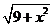 ,⊙B半径为│x+2│,
,⊙B半径为│x+2│,
①设⊙B与⊙A外切,则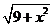 =│x+2│+1,
=│x+2│+1,
当x>-2时,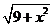 =x+3,平方化简得:x=0符题意,∴B(0,0),
=x+3,平方化简得:x=0符题意,∴B(0,0),
当x<-2时,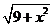 =-x-1,化简得x=4>-2(舍),
=-x-1,化简得x=4>-2(舍),
②设⊙B与⊙A内切,则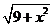 =│x+2│-1,
=│x+2│-1,
当x>-2时,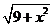 =x+1,得x=4>-2,∴B(4,0),
=x+1,得x=4>-2,∴B(4,0),
当x<-2时,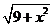 =-x-3,得x=0,
=-x-3,得x=0,
知识点七、正多边形和圆
重点:讲清正多边形和圆中心正多边形半径、中心角、弦心距、边长之间的关系.
难点:使学生理解四者:正多边形半径、中心角、弦心距、边长之间的关系.
正多边形的中心:所有对称轴的交点;
正多边形的半径:正多边形外接圆的半径。
正多边形的边心距:正多边形内切圆的半径。
正多边形的中心角:正多边形每一条边所对的圆心角。
正n边形的n条半径把正n边形分成n个全等的等腰三角形,每个等腰三角形又被相应的边心距分成两个全等的直角三角形。
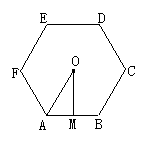
例1.如图,已知正六边形ABCDEF,其外接圆的半径是a,求正六边形的周长和面积.
解题思路:要求正六边形的周长,只要求AB的长,已知条件是外接圆半径,因此自然而然,边长应与半径挂上钩,很自然应连接OA,过O点作OM⊥AB垂于M,在Rt△AOM中便可求得AM,又应用垂径定理可求得AB的长.正六边形的面积是由六块正三角形面积组成的.
解:如图所示,由于ABCDEF是正六边形,所以它的中心角等于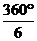 =60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
 因此,所求的正六边形的周长为6a
因此,所求的正六边形的周长为6a
在Rt△OAM中,OA=a,AM=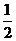 AB=
AB=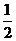 a
a
利用勾股定理,可得边心距
OM=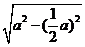 =
=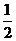
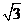 a
a
∴所求正六边形的面积=6×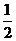 ×AB×OM=6×
×AB×OM=6×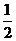 ×a×
×a×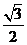 a=
a=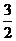
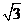 a2
a2
例2.在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6.
(1)求△ABC的边AB上的高h.
(2)设DN=x,且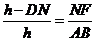 ,当x取何值时,水池DEFN的面积最大?
,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
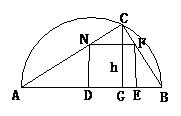
解题思路:要求矩形的面积最大,先要列出面积表达式,再考虑最值的求法,初中阶段,尤其现学的知识,应用配方法求最值.(3)的设计要有新意,应用圆的对称性就能圆满解决此题.
解:(1)由AB·CG=AC·BC得h=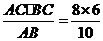 =4.8
=4.8
(2)∵h=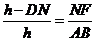 且DN=x
且DN=x
∴NF=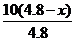
则S四边形DEFN=x·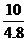 (4.8-x)=-
(4.8-x)=- x2+10x
x2+10x
=- (x2-
(x2-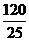 x)
x)
=- [(x-
[(x-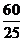 )2-
)2-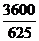 ]
]
=-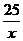 (x-2.4)2+12
(x-2.4)2+12
∵-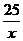 (x-2.4)2≤0
(x-2.4)2≤0
∴-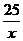 (x-2.4)2+12≤12 且当x=2.4时,取等号
(x-2.4)2+12≤12 且当x=2.4时,取等号
∴当x=2.4时,SDEFN最大.
(3)当SDEFN最大时,x=2.4,此时,F为BC中点,在Rt△FEB中,EF=2.4,BF=3.
∴BE=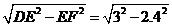 =1.8
=1.8
∵BM=1.85,∴BM>EB,即大树必位于欲修建的水池边上,应重新设计方案.
∵当x=2.4时,DE=5
∴AD=3.2,
由圆的对称性知满足条件的另一设计方案,如图所示:
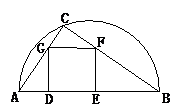
此时,AC=6,BC=8,AD=1.8,BE=3.2,这样设计既满足条件,又避开大树.
练习1如图所示,已知⊙O的周长等于6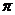 cm,求以它的半径为边长的正六边形ABCDEF的面积.
cm,求以它的半径为边长的正六边形ABCDEF的面积.
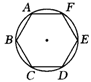
4.如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.
(1)若点B坐标为(4,0),⊙B半径为3,试判断⊙A与⊙B位置关系;
 (2)若⊙B过M(-2,0)且与⊙A相切,求B点坐标.
(2)若⊙B过M(-2,0)且与⊙A相切,求B点坐标.
答案: 1.B 2.D 3.B
2.半径为2cm和1cm的⊙O1和⊙O2相交于A、B两点,且O1A⊥O2A,则公共弦AB的长为( ).
A.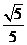 cm B.
cm B.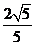 cm C.
cm C.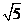 cm D.
cm D.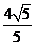 cm
cm
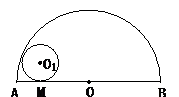 3.如图所示,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是( ).
3.如图所示,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是( ).
A.y=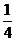 x2+x B.y=-
x2+x B.y=-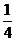 x2+x
x2+x
C.y=-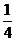 x2-x D.y=
x2-x D.y=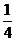 x2-x
x2-x
3.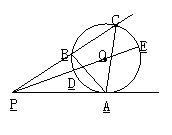 如图,P为⊙O外一点,PA切⊙O于点A,过点P的任一直线交⊙O于B、C,连结AB、AC,连PO交⊙O于D、E.
如图,P为⊙O外一点,PA切⊙O于点A,过点P的任一直线交⊙O于B、C,连结AB、AC,连PO交⊙O于D、E.
(1)求证:∠PAB=∠C.
(2)如果PA2=PD·PE,那么当PA=2,PD=1时,求⊙O的半径.
答案: 1.A 2.B 3. (1)提示:作直径AF,连BF,如右图所示.
(2)由已知PA2=PD·PE,可得⊙O的半径为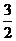 .
.
知识点六、圆与圆的位置关系
.重点:两个圆的五种位置关系中的等价条件及它们的运用.
难点:探索两个圆之间的五种关系的等价条件及应用它们解题.
外离:两圆没有公共点,一个圆上所有的点都在另一个圆的外部
相离:
内含:两圆没有公共点,一个圆上所有的点都在另一个圆的内部
相切:
外切:两圆只有一个公共点,除公共点外一个圆上所有的点都在另一个圆的外部
内切:两圆只有一个公共点,除公共点 外一个圆上所有的点都在另一个圆的内部
外一个圆上所有的点都在另一个圆的内部
相交 :两圆只有两个公共点。
设两圆的半径分别为r1、r2,圆心距(两圆圆心的距离)为d,则有两圆的位置关系,d与r1和r2之间的关系.
外离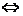 d>r1+r2
d>r1+r2
外切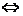 d=r1+r2
d=r1+r2
相交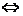 │r1-r2│<d<r1+r2
│r1-r2│<d<r1+r2
内切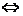 d=│r1-r2│
d=│r1-r2│
内含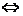 0≤d<│r1-r2│(其中d=0,两圆同心)
0≤d<│r1-r2│(其中d=0,两圆同心)
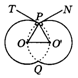
例1.两个同样大小的肥皂 泡黏在一起,其剖面如图1所示(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.
泡黏在一起,其剖面如图1所示(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.
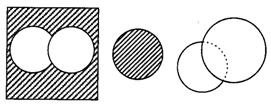
(1)
 (2)
(2)
解题思路:要求∠TPN,其实就是求∠OPO′的角度,很明显,∠POO′是正三角形,如图2所示.
解:∵PO=OO′=PO′
∴△PO′O是一个等边三角形
∴∠OPO′=60°
又∵TP与NP分别为两圆的切线,
∴∠TPO=90°,∠NPO′=90°
∴∠TPN=360°-2×90°-60°=120°
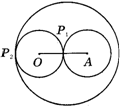
例2.如图1所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
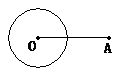
(1) (2)
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
解题思路:(1)作⊙A和⊙O外切,就是作以A为圆心的圆与⊙O的圆心距d=rO+rA;(2)作OA与⊙O相内切,就是作以A为圆心的圆与⊙O的圆心距d=rA-rO.
解:如图2所示,(1)作法:以A为圆心,rA=15-7=8为半径作圆,则⊙A的半径为8cm
(2)作法:以A点为圆心,rA′=15+7=22为半径作圆,则⊙A的半径为22cm
练习:1.已知两圆的半径分别为5cm和7cm,圆心距为8cm,那么这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2.如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA_______,PB=________,PC=_______AC=______,BC=______∠AOB=________.
2.设I是△ABC的内心,O是△ABC的外心,∠A=80°,则∠BIC=________,∠BOC=________.
答案1.A 2. 130° 160°
知识点五、直线和圆的位置关系:相交、相切、相离
重点:,直线和圆的位置关系的性质和判定
难点:直线和圆三种位置关系的性质及判定。
当直线和圆相交时,d<r;反过来,当d<r时,直线和圆相交。
当直线和圆相切时,d=r;反过来,当d=r时,直线和圆相切。
当直线和圆相离时,d>r;反过来,当d>r时,直线和圆相离。
切线的性质定理:圆的切线垂直于过切点的直径
切线的判定定理:经过直径的一端,并且垂直于这条直径的直线是圆的切线。
切线长:在经过圆外一点的圆的切线上,这点到切点之间的线段的长叫做这点到圆的切线长。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和圆外这点的连线平分两条切线的夹角。
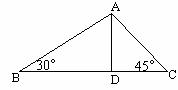
例1、 在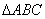 中,BC=6cm,∠B=30°,∠C=45°,以A为圆心,当半径r多长时所作的⊙A与直线BC相切?相交?相离?
中,BC=6cm,∠B=30°,∠C=45°,以A为圆心,当半径r多长时所作的⊙A与直线BC相切?相交?相离?
解题思路:作AD⊥BC于D
在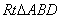 中,∠B=30° ∴
中,∠B=30° ∴ 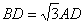
在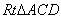 中,∠C=45°
中,∠C=45°
∴ CD=AD
∵ BC=6cm ∴ 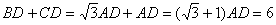
∴ 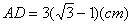
∴ 当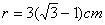 时,⊙A与BC相切;当
时,⊙A与BC相切;当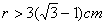 时,⊙A与BC相交;当
时,⊙A与BC相交;当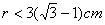 时,⊙A与BC相离。
时,⊙A与BC相离。
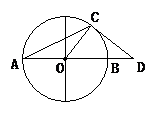
例2.如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.
(1)CD与⊙O相切吗?如果相切,请你加以证明,如果不相切,请说明理由.
(2)若CD与⊙O相切,且∠D=30°,BD=10,求⊙O的半径.
解题思路:(1)要说明CD是否是⊙O的切线,只要说明OC是否垂直于CD,垂足为C,因为C点已在圆上.
由已知易得:∠A=30°,又由∠DCB=∠A=30°得:BC=BD=10
解:(1)CD与⊙O相切
 理由:①C点在⊙O上(已知)
理由:①C点在⊙O上(已知)
②∵AB是直径
∴∠ACB=90°,即∠ACO+∠OCB=90°
∵∠A=∠OCA且∠DCB=∠A
∴∠OCA=∠DCB
∴∠OCD=90°
综上:CD是⊙O的切线.
(2)在Rt△OCD中,∠D=30°
∴∠COD=60°
∴∠A=30°
∴∠BCD=30°
∴BC=BD=10
∴AB=20,∴r=10
答:(1)CD是⊙O的切线,(2)⊙O的半径是10.
练习:1.如图,AB为⊙O直径,BD切⊙O于B点,弦AC的延长线与BD交于D点,若AB=10,AC=8,则DC长为________.
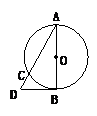

5、三角形的内心:三角形三条角平分线的交点,即三角形内切圆的圆心。
例1.如图,通过防治“非典”,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图24-49所示,A、B、C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.
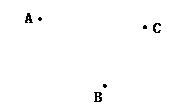
解题思路: 连结AB、BC,作线段AB、BC的中垂线,两条中垂线的交点即为垃圾回收站所在的位置.
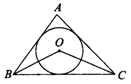 例2.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,
例2.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,
则∠BOC=( )
A.130° B.100° C.50° D.65°
解题思路:此题解题的关键是弄清三角形内切圆的圆心是三角形内角平分线的交点,答案A
 例3.如图,Rt△ABC,∠C=90°,AC=3cm,BC=4cm,则它的外心与顶点C的距离为(
).
例3.如图,Rt△ABC,∠C=90°,AC=3cm,BC=4cm,则它的外心与顶点C的距离为(
).
A.5 cm B.2.5cm C.3cm D.4cm
解题思路:直角三角形外心的位置是斜边的中点,答案 B
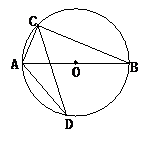 练习1、如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平
练习1、如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平
分∠ACB,则弦AD长为( )
A.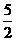
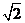 B.
B.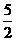 C.
C.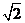 D.3
D.3
4、三角形的内切圆:与三角形的三边都相切的圆。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com