
21.(本小题满分8分)
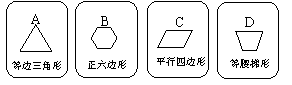
有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图).小明将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
⑴用树状图(或列表法)表示两次模牌所有可能出现的结果(纸牌可用A、B、C、D表示);
⑵求摸出两张牌面图形都是中心对称图形的纸牌的概率.
20. (本小题满分8分)
(本小题满分8分)
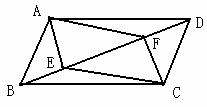
如图,E、F是□ABCD对角线BD上的两点,给出下列三个条件:⑴BE=DF;⑵∠AEB=∠DFC;⑶AF∥EC.请你从中选择一个条件,能使四边形AECF是平行四边形的选法有 _________种,请选择一种加以证明.
19.解答下列各题(本题有4小题,每题4分,共16分.)
⑴计算: 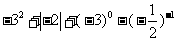
⑵ 化简: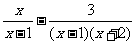 ,并选一个你喜欢的x值代入求值
,并选一个你喜欢的x值代入求值
(3)解不等式组 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
(4)解方程 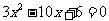
18.如图,对面积为s的△ABC逐次进行以下操作:第一次操作,
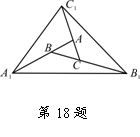 分别延长AB、BC、CA至点
分别延长AB、BC、CA至点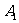 、
、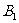 、
、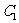 ,使得
,使得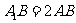 ,,
,,
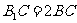
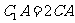 顺次连接
顺次连接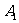 、
、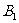 、
、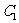 ,得到△
,得到△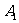
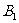
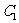 ,
,
记其面积为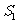 ;第二次操作,分别延长
;第二次操作,分别延长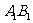 ,
,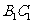 ,
,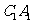 至点
至点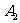 、
、
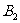 、
、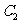 ,使得
,使得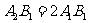 ,
,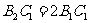 ,
,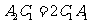 ,
,
顺次连接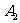 、
、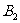 、
、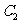 ,得到△
,得到△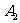
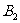
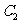 2,记其面积为
2,记其面积为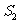 ;…;
;…;
按此规律继续下去,可得到△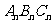 ,则其面积
,则其面积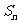 .
.
17. 在直角坐标系中,直线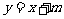 与双曲线
与双曲线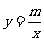 在第一象
在第一象
限交于点A,与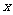 轴交于点C,AB⊥
轴交于点C,AB⊥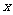 轴,垂足为B,且
轴,垂足为B,且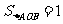 ;
;
则⊿ABC的面积为
16. 如图,在直角坐标系中,点A在y轴上,△OAB是等腰直角三角
形,斜边OA=2,将△OAB绕点O逆时针旋转90°得△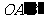 ,则点
,则点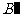
的坐标为 .
15.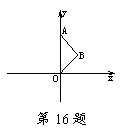 如图,在△ABC内有边长分别为8,6,
如图,在△ABC内有边长分别为8,6,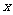 的三个小等边三角形⊿DCE、⊿FEG、⊿HGP,且点
的三个小等边三角形⊿DCE、⊿FEG、⊿HGP,且点
D、F、H在边AB上,点E、G、P在边BC上,则x的值为_______.
14.如图,AB是⊙O的直径,AB=4,点C是半圆的三等分点,点D是中点,AB上一动点P,连
接PC,PD,则PC+PD的最小值是 .
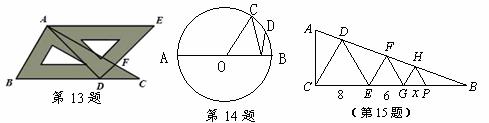
13.将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是 .
12.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再捕捞第二次鱼共200条,有10条做了记号,则估计湖里有 条鱼.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com