
2.下列n的取值中,使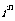 =1(i是虚数单位)的是
=1(i是虚数单位)的是
A.n=2 B .n=3 C .n=4 D .n=5
[答案]C
[解析]因为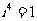 ,故选C.
,故选C.
1.已知全集U=R,则正确表示集合M= {-1,0,1} 和N= {
x |x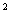 +x=0} 关系的韦恩(Venn)图是
+x=0} 关系的韦恩(Venn)图是
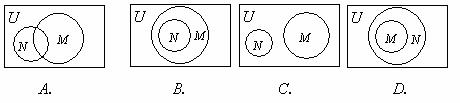
[答案]B
[解析]由N= {
x |x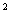 +x=0}
+x=0}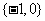 得
得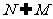 ,选B.
,选B.
56、迄今为止,人类历史上爆发了两次世界大战,世界格局也在发生着变化。请问:
(1)第一次世界大战后,帝国主义列强建立了什么体系,暂时稳定了世界局势?(2分)
(2)第二次世界大战后,形成了什么世界政治格局?(2分)
(3)“冷战”结束后世界政治格局的发展方向是什么? (2分)
(4)各国要在世界格局变化中占据有利地位,具有决定性作用的是什么? (2分)
28.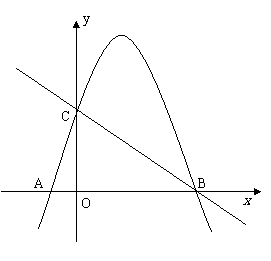 (本题满分12分)
(本题满分12分)
如图,已知抛物线与x轴交于A(-1,0)、B(4,0)两点,
与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)求直线BC的函数解析式;
(3)在抛物线上,是否存在一点P,使△PAB的面积等于
△ABC的面积,若存在,求出点P的坐标,若不存在,
请说明理由.
(4)点Q是直线BC上的一个动点,
若△QOB为等腰三角形,请写出此时
点Q的坐标.(可直接写出结果)
27. (本题满分12分)
如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
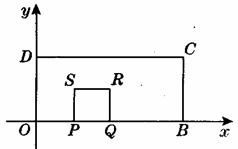 (1)P是OB上一个动点,动点 Q在 PB或其延长线上运动,OP=PQ,作以 PQ为一边的正方形PQRS,点P从O点开始沿射线OB方向运动,直到点P与点B重合,设OP=x,正方形PQRS与矩形OBCD重叠部分的面积为y,写出y与x的函数关系式;
(1)P是OB上一个动点,动点 Q在 PB或其延长线上运动,OP=PQ,作以 PQ为一边的正方形PQRS,点P从O点开始沿射线OB方向运动,直到点P与点B重合,设OP=x,正方形PQRS与矩形OBCD重叠部分的面积为y,写出y与x的函数关系式;
(2)在(1)中,当x分别取1和3时,y的值分别是多少?
(3)已知直线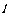 :y=ax-a都经过一定点A,求经过定点A且把矩形OBCD面积平均分成两部分的直线的关系式.
:y=ax-a都经过一定点A,求经过定点A且把矩形OBCD面积平均分成两部分的直线的关系式.
26.(本题满分10分)
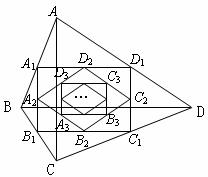 四边形ABCD中,
四边形ABCD中,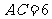 ,
,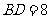 且
且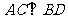 顺次连接四边形
顺次连接四边形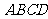 各边中点,得到四边形
各边中点,得到四边形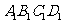 ;再顺次连接四边形
;再顺次连接四边形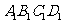 各边中点,得到四边形
各边中点,得到四边形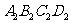 ……如此进行下去得到四边形
……如此进行下去得到四边形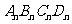 .
.
(1)猜测四边形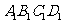 的形状并加以证明;
的形状并加以证明;
(2)写出四边形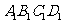 和四边形
和四边形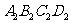 的面积;
的面积;
(3)写出四边形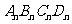 的面积;
的面积;
(4)求四边形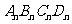 的周长.
的周长.
25.(本题满分8分)
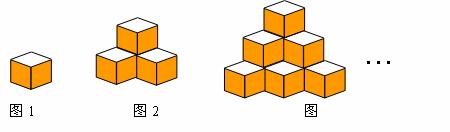
图1是棱长为a的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层的小正方体的个数为s.解答下列问题:
(1)按照要求填表:
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|||||
|
s |
1 |
3 |
6 |
|
… |
|||||
|
n |
1 |
2 |
3 |
4 |
… |
|
s |
1 |
3 |
6 |
|
… |
|
n |
1 |
2 |
3 |
4 |
… |
|
s |
1 |
3 |
6 |
|
… |
(2)写出当n=10时,s = .
(3)根据上表中的数据,把s作为纵坐标,n作为横坐标,在平面直角坐标系中描出相应的各点.
(4)合情猜想符合这图形的函数解析式,求出该函数的解析式,并验证这些点的坐标是否满足函数解析式。
24.(本小题满分8分)
某市经济开发区建有B、C、D三个食品加工厂, 这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上, 它们之间有公路相通, 且AB=CD=900米, AD=BC=1700米. 自来水公司已经修好一条自来水主管道AN, B、C两厂之间的公路与自来水管道交于E处, EC=500米. 若修建自来水主管道到各工厂的自来水管道由各厂负责, 每米造价800元.
(1)要使修建自来水管道的造价最低, 这三个工厂的自来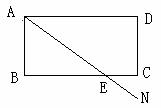
水管道路线应怎样设计? 请在图中画出;
(2)求出各厂所修建自来水管道的最低造价各是多少元?
23.(本小题满分6分)
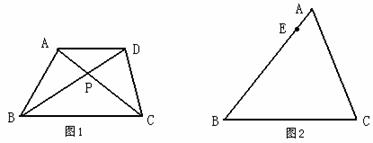
如图1,在梯形ABCD中AD∥BC,对角线AC,BD交于点P,则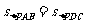 ,请你用梯形对角线的这一特殊性质,解决下面问题。
,请你用梯形对角线的这一特殊性质,解决下面问题。
在图2中,点E是⊿ABC中AB边上的任意一点,且AE≠BE,过点E画一条直线,把⊿ABC分成面积相等的两部分,保留作图痕迹,并简要说明你的方法。
22.(本小题满分8分)
2009年4月,某县体质监测中心等机构开展了青少年形体测评.专家组随机抽查了我县若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
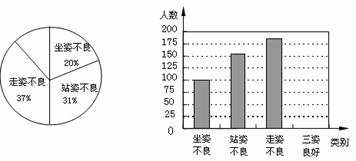
(1)请将两幅统计图补充完整;
(2)在这次形体测评中,一共抽查了 名学生,如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人;
 (3)根据统计结果,请你简单谈谈自己的看法.
(3)根据统计结果,请你简单谈谈自己的看法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com