
20. ( 本大题16分,第一小题5分,第二小题5分,第三小题6分)
已知公差大于零的等差数列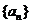 的前n项和为Sn,且满足:
的前n项和为Sn,且满足: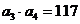 ,
,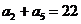 .
.
(1)求数列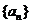 的通项公式
的通项公式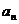 ;
;
(2)若数列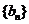 是等差数列,且
是等差数列,且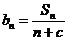 ,求非零常数c;
,求非零常数c;
(3)若(2)中的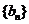 的前n项和为
的前n项和为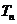 ,求证:
,求证: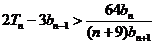
数学附加题
(时间30分钟,满分40分)
19. ( 本大题16分,第一小题5分,第二小题5分,第三小题6分)
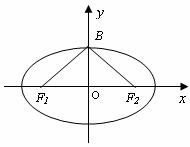
如图,已知椭圆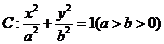 的焦点和上顶点分别为
的焦点和上顶点分别为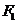 、
、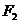 、
、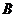 ,我们称
,我们称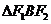 为椭圆
为椭圆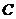 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
 (1)已知椭圆
(1)已知椭圆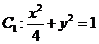 和
和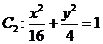 ,判断
,判断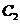 与
与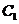 是否
是否
相似,如果相似则求出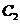 与
与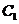 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)写出与椭圆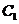 相似且半短轴长为
相似且半短轴长为 的椭圆
的椭圆 的方程,并列举
的方程,并列举
相似椭圆之间的三种性质(不需证明);
(3)已知直线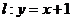 ,在椭圆
,在椭圆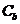 上是否存在两点
上是否存在两点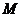 、
、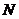 关于直
关于直
线 对称,若存在,则求出函数
对称,若存在,则求出函数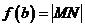 的解析式.
的解析式.
18. ( 本大题15分,第一小题7分,第二小题8分)
⑴在长度为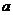 的线段
的线段 上任意作一点
上任意作一点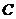 ,求
,求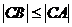 的概率;
的概率;
⑵若将长度为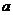 的线段截成三段,则三段长能围成一个三角形的概率有多大.
的线段截成三段,则三段长能围成一个三角形的概率有多大.
17.( 本大题15分,第一小题7分,第二小题8分)
已知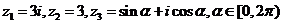 ,
,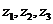 在平面上对应的点
在平面上对应的点
为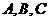 .
.
(1)若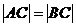 ,求
,求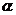 的值;
的值;
(2)若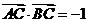 ,求
,求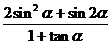 的值.
的值.
16. ( 本大题14分,第一小题7分,第二小题7分)
已知二次函数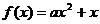 ,若对任意x
,若对任意x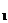 、x
、x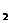 ∈R,恒有2f(
∈R,恒有2f(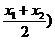 ≤f(x
≤f(x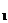 )+f(x
)+f(x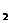 )成立,不等式f(x)<0的解集为A.
)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合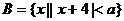 ,若集合B是集合A的子集,求
,若集合B是集合A的子集,求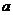 的取值范围.
的取值范围.
15.(本大题14分,第一小题7分,第二小题7分)
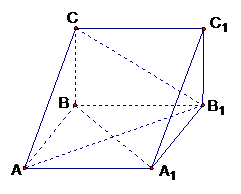
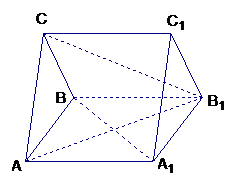 如图,在三棱柱
如图,在三棱柱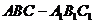 中,四边形
中,四边形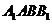 为菱形,
为菱形,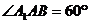 ,四边形
,四边形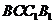 为矩形,若
为矩形,若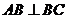 且
且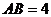 ,
,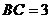
⑴求证:平面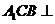 平面
平面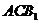 ;
;
⑵求三棱柱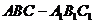 的体积.
的体积.
14. 三位同学合作学习,对问题“已知不等式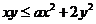 对于
对于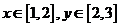 恒成立,求
恒成立,求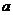 的取值范围”提出了各自的解题思路.
的取值范围”提出了各自的解题思路.
甲说:“可视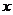 为变量,
为变量,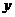 为常量来分析”.
为常量来分析”.
乙说:“寻找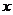 与
与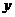 的关系,再作分析”.
的关系,再作分析”.
丙说:“把字母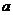 单独放在一边,再作分析”.
单独放在一边,再作分析”.
参考上述思路,或自已的其它解法,可求出实数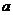 的取值范围是
.
的取值范围是
.
13. 已知函数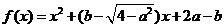 是偶函数,则函数图像与
是偶函数,则函数图像与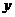 轴交点的纵坐标的最大值是
.
轴交点的纵坐标的最大值是
.
12. 已知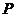 为抛物线
为抛物线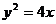 上一点,设
上一点,设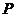 到准线的距离为
到准线的距离为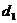 ,
,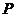 到点
到点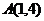 的距离为
的距离为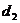 ,则
,则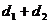 的最小值为________.
的最小值为________.
11. 定义:若对定义域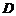 上的任意实数
上的任意实数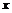 都有
都有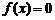 ,则称函数
,则称函数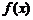 为
为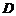 上的零函数.根据以上定义,“
上的零函数.根据以上定义,“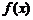 是
是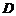 上的零函数或
上的零函数或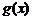 是
是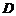 上的零函数”为“
上的零函数”为“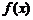 与
与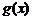 的积函数是
的积函数是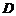 上的零函数”的 条件.
上的零函数”的 条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com