
杭州学军中学高三年级2006学年第三次月考
数学试卷(文科)
一、选择题:(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合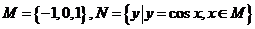 ,则
,则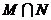 是
( )
是
( )
(A)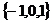 (B)
(B)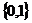 (C)
(C)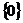 (D)
(D)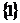
2.若条件 ,条件
,条件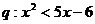 ,则
,则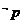 是
是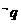 的txjy
的txjy
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分又不必要条件
3.定义域为R的函数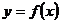 的值域为
的值域为 ,则函数
,则函数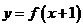 的值域为 ( )
的值域为 ( )
(A) (B)
(B)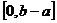 (C)
(C) (D)
(D)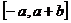
4.函数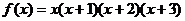 …
…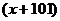 在
在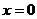 处导数值为 ( )
处导数值为 ( )
(A)0 (B)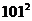 (C)1
(D)
(C)1
(D)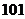 !
!
5.设函数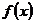 是定义在R上的以3为周期的奇函数,若
是定义在R上的以3为周期的奇函数,若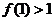 ,
, ,
,
则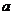 取值范围是
( )
取值范围是
( )
(A)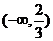 (B)
(B)
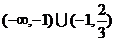
(C) 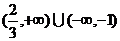 (D)
(D)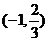
6.下列命题正确的是( )
(A)函数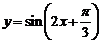 在区间
在区间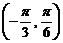 内单调递增
内单调递增
(B)函数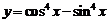 的最小正周期为
的最小正周期为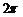
(C)函数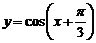 的图像是关于点
的图像是关于点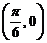 成中心对称的图形
成中心对称的图形
(D)函数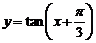 的图像是关于直线
的图像是关于直线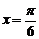 成轴对称的图形
成轴对称的图形
7.已知等比数列 的公比
的公比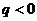 ,前
,前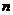 项的和为
项的和为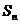 ,则
,则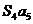 与
与 的大小关系
的大小关系
(A) (B)
(B)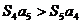 (C)
(C)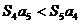 (D)不确定
(D)不确定
8.袋中有40个小球,其中红色球16个、蓝色球12个、白色球8个、黄色球4个,从中随机抽取10球作成一个样本,则这个样本恰好是按分层抽样得到的概率为 ( )
(A)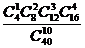 (B)
(B)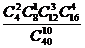 (C)
(C)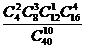 (D)
(D)
9.使关于 的不等式
的不等式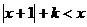 有解的实数
有解的实数 的取值范围是
( )
的取值范围是
( )
(A)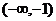 (B)
(B) (C)
(C)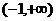 (D)
(D)
10.已知函数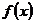 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的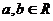 ,满足
,满足
下列结论:①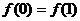 ,②
,②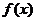 为偶函数;③数列
为偶函数;③数列 为等比数列;④数列
为等比数列;④数列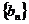 为等差数列。其中正确的是
( )
为等差数列。其中正确的是
( )
(A)①② (B)②④ (C)①③④ (D)①②③④
二、填空题:本大题共4小题,每小题4分,共16分。
11.若指数函数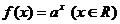 的部分对应值如下表
的部分对应值如下表

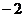
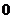
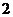
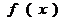

1
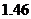
则不等式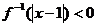 的解集为____________。
的解集为____________。
12.函数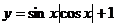 的最小正周期与最大值的和为 。
的最小正周期与最大值的和为 。
13.设等差数列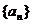 的前n项和为Sn,若
的前n项和为Sn,若 ,则
,则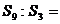 。
。
14.已知奇函数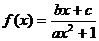 有最大值
有最大值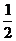 , 且
, 且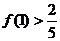 , 其中实数
, 其中实数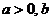 是正整数.
是正整数.
则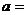 ____________
____________ 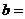 .
. 。
。

 杭州学军中学高三年级2006学年第三次月考
杭州学军中学高三年级2006学年第三次月考
数学答卷(文科)
座位号
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:本大题共4小题;每小题4分,共16分。
11. 12.
13. 14.
三、解答题:本大题共6小题,每小题14分,共84分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分14分)
设集合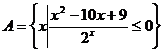
 ,若
,若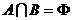 ,求实数
,求实数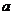 的取值范围.
的取值范围.
16..(本小题满分14分)
已知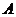 、
、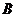 、
、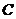 三点的坐标分别为
三点的坐标分别为 、
、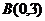 、
、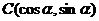 ,
,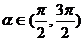 ,
,
(1)若 ,求角
,求角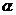 的值;
的值;
(2)若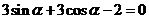 ,求
,求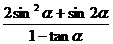 的值。
的值。
17.(本小题满分14分)
已知函数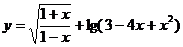 的定义域为
的定义域为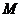 ,当
,当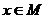 时,
时,
求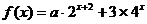
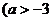 )的最小值。
)的最小值。
18.(本小题满分14分)
已知数列 的前
的前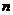 项和为
项和为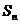 ,若
,若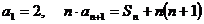 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)令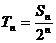 ,问数列
,问数列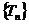 是否有最大的项,若存在则求出最大项的值;若不存在则说明理由。
是否有最大的项,若存在则求出最大项的值;若不存在则说明理由。
19.(本小题满分14分)
已知函数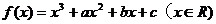 在
在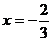 处取得极值,其图象在点
处取得极值,其图象在点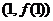 处的切线与直线
处的切线与直线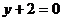 平行
平行
(1)求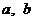 的值;
的值;
(2)若对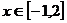 都有
都有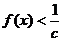 恒成立,求
恒成立,求 的取值范围。
的取值范围。

 20.(本小题满分14分)
20.(本小题满分14分)
已知二次函数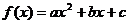 和一次函数
和一次函数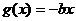 其中
其中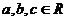 且
且
满足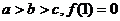 .
.
(1)证明:函数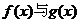 的图象交于不同的两点A,B;
的图象交于不同的两点A,B;
(2)若函数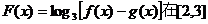 上的最小值为2,最大值为3,求
上的最小值为2,最大值为3,求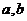 值;
值;
(3)求线段AB在 轴上的射影A1B1的长的取值范围.
轴上的射影A1B1的长的取值范围.
一、选择题:(本题每小题5分,共50分)
1
2
3
4
5
6
7
8
9
10
D
B
C
D
D
C
B
A
A
C
二、填空题:(本题每小题4分,共16分)
11. 12.
12. 13.
13. 14.
14.
三、解答题(本大题6小题,共84分。解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分14分)
解 得
得 …………………4分
…………………4分
又

∵
 +1>
+1> 得B={y|y<
得B={y|y< 或y>
或y>
 +1}……………………8分
+1}……………………8分
∵A∩B=φ
 ∴
∴ 
 1
1

 +1
+1 9…………………12分
9…………………12分
∴
 -2
-2 …………………14分
…………………14分
16.(本小题满分14分)
解:(1) ,
,
由 得
得 又
又
 ………6分
………6分
(2)因

 ………8分
………8分
又 ,
, ,则
,则
即 …………………10分
…………………10分

 …14分
…14分
17.(本小题满分14分)
解: (…………………3分)
(…………………3分)
 =
= (…………………7分)
(…………………7分)
又 ,
, ,
,
(1)若 ,即
,即 时,
时, =
= =
= ,(…………10分)
,(…………10分)
(2)若 ,即
,即
 时,
时,
所以当 即
即 时,
时, =
= (…………………13分)
(…………………13分)
 (…………………14分)
(…………………14分)
18.(本小题满分14分)
解:(1)令 ,
, ,即
,即
由

∵ ,∴
,∴ ,即数列
,即数列 是以
是以 为首项、
为首项、 为公差的等差数列, ∴
为公差的等差数列, ∴ …………8分
…………8分
(2) 化简得
化简得 ,即
,即
∵ ,又∵
,又∵ 时,
时, …………12分
…………12分
∴各项中最大项的值为 …………14分
…………14分
19.(本小题满分14分)
解:(1) ,由题意
,由题意 ―――①
―――①
又 ―――②
―――②
联立得 …………5分
…………5分
(2)依题意得 即
即 ,对
,对 恒成立,设
恒成立,设 ,则
,则
解 得
得
当  ……10分
……10分
则
又 ,所以
,所以 ;故只须
;故只须  …………12分
…………12分
解得
即 的取值范围是
的取值范围是 …………14分
…………14分
20.(本小题满分14分)
解:(1)由 ,
,
 即函数
即函数 的图象交于不同的两点A,B; ……4分(2)
的图象交于不同的两点A,B; ……4分(2)
已知函数 ,
, 的对称轴为
的对称轴为 ,
,
故 在[2,3]上为增函数,
……………6分
在[2,3]上为增函数,
……………6分
 ……8分
……8分
(3)设方程
 ……10分
……10分
 ……12分
……12分
设 的对称轴为
的对称轴为 上是减函数,
上是减函数, ……14分
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com