YCY
1.已知复数 ,
, ,那么
,那么 =
=
2.若 ,则
,则 =
=
3.向量 的单位向量是
的单位向量是
4.五个数1,2,3,4,a的平均数是3,这五个数的标准差是
5.设 为曲线
为曲线 上一点,曲线
上一点,曲线 在点
在点 处的切线的斜率的范围是
处的切线的斜率的范围是 ,则点
,则点 纵坐标的取值范围是____ __
纵坐标的取值范围是____ __
6.在下面等号右侧两个分数的分母括号处,各填上一个自然数,使等式成立且这两个自然数的和最小: ,所填自然数分别为
,所填自然数分别为
7.在△ABC中,AB=2,AC=1,D为BC中垂线上任意一点,则 =________
=________
8.对一切实数 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
9.已知 的外接圆的圆心
的外接圆的圆心 ,
, ,则
,则 的大小关系为__ ___
的大小关系为__ ___
 10.用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
10.用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
则它的体积的最大值与最小值之差为
11.在约束条件 下,当
下,当 时,目标函数
时,目标函数 的最大值的变化范围是
的最大值的变化范围是
12.已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是准线上一点,且
是准线上一点,且 ,
, ,则双曲线的离心率是
,则双曲线的离心率是
13.已知 ,
, ,对任意
,对任意 ,经过两点
,经过两点 的直线与一定圆相切,则圆方程为
的直线与一定圆相切,则圆方程为
14. 在等比数列{an}中, 且a8>a9,则使得
且a8>a9,则使得 的自然数
的自然数 的最大值为__________
的最大值为__________
二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.
试题详情
已知向量 设函数
设函数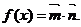
试题详情
(I)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
试题详情
(II)在△ABC中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值
的值
试题详情
试题详情
 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
求证:(1)AC1∥平面BDE;(2)A1E^平面BDE.
试题详情
试题详情
徐州、苏州两地相距500千米,一辆货车从徐州匀速行驶到苏州,规定速度不得超过100千米/小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为0.01;固定部分为a元(a>0).
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
试题详情
试题详情
试题详情
(1)求 ; (2)求数列{
; (2)求数列{  }的通项公式;
}的通项公式;
试题详情
试题详情
试题详情
若椭圆 过点(-3,2),离心率为
过点(-3,2),离心率为 ,⊙O的圆心为原点,直径
,⊙O的圆心为原点,直径
试题详情
为椭圆的短轴,⊙M的方程为 ,过⊙M上任一点P作⊙O的切线PA、
,过⊙M上任一点P作⊙O的切线PA、
PB,切点为A、B.
(I)求椭圆的方程;
(II)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
试题详情
(III)求 的最大值与最小值.
的最大值与最小值.
试题详情
试题详情
设函数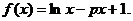
试题详情
(I)求函数 的极值点;
的极值点;
试题详情
试题详情
(III)证明: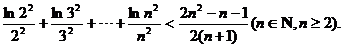
2009届高三南通市二模模拟考试五校联考数学试题
参 考 答 案
试题详情
试题详情
试题详情
9.  10. 6
11.
10. 6
11.

试题详情
12.  13.
13.
 14. 8
14. 8
试题详情
15.解:(I)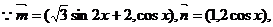
试题详情
试题详情
 …………4分
…………4分
试题详情
 …………5分
…………5分
试题详情
试题详情
 …………7分
…………7分
试题详情
(II)由 得
得
试题详情
试题详情
试题详情
试题详情
 …………10分
…………10分
试题详情
试题详情
 …………12分
…………12分
试题详情
试题详情
 …………14分
…………14分
试题详情
16. (1)证明:连接AC,设AC∩BD=O.由条件得ABCD为正方形,故O为AC中点.因为E为CC1中点,所以OE∥AC1.因为OEÌ平面BDE,AC1(/平面BDE.所以AC1∥平面BDE.
(2)连接B1E.设AB=a,则在△BB1E中,BE=B1E=a,BB1=2a.所以BE2+B1E2=BB12.所以B1E^BE.由正四棱柱得,A1B1^平面BB1C1C,所以A1B1^BE.所以BE^平面A1B1E.所以A1E^BE.同理A1E^DE.所以A1E^平面BDE.
试题详情
17. 解:(1)依题意知汽车从甲地匀速行驶到乙地所用时间为 ,全程运输成本为
,全程运输成本为 ……………………………………….4分
……………………………………….4分
试题详情
故所求函数及其定义域为 ………………………….6分
………………………….6分
试题详情
(2)依题意知a,v都为正数,故有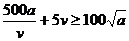
试题详情
当且仅当 .即
.即 时上式中等号成立………………………...8分
时上式中等号成立………………………...8分

