
宁夏石嘴山市2009年高三联考数学试题(文科)
命题:孙建国 王万波 卢尚义 马志敏
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22―24题为选考题,其它题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡上的指定位置上。
2.选择题答案使用2B铅笔填涂;如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题必使用0.5毫米的黑色中性(签字)笔或炭素笔书写,字体工整、笔迹清楚。
3.按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不要折叠、不破损。
5.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
样本数据 ,
,
 ,
, 的标准差
的标准差

 其中
其中 表示球的半径
表示球的半径
 为样本平均数
为样本平均数
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题5分,共60分。每小题只有一个正确答案)
1.sin660 的值是
的值是
A. B.
B.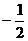 C.
C. D.
D.
2.设全集 则右图中阴影部分表示的集合为
则右图中阴影部分表示的集合为
 A.
A. B.
B.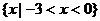
C.{x|x>0} D.
3. 等比数列{an}中,a4=4,则 等于( )
等于( )
A.4 B.
4. 相切,且在两坐标轴上截距相等的直线有
相切,且在两坐标轴上截距相等的直线有
A.2条 B.3条 D.4条 D.6条
5. 若 =(2,
-3),
=(2,
-3),
 =(1,
-2),向量
=(1,
-2),向量 满足
满足 ^
^ ,
, ?
? =1,则
=1,则 的坐标是
的坐标是
A.(3,-2) B.(3, 2) C.(-3, -2) D.(-3, 2)
 6. 已知a,b都是实数,那么“
6. 已知a,b都是实数,那么“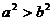 ”是“
”是“ ”的 ( )
”的 ( )

A.充分而不必要条件
B.必要而不充分条件

C.充分必要条件
D.既不充分与不必要条件
7.在可行域内任取一点,如框图所示进行操作,则能输出数对 的概率是
的概率是
A. B.
B.
C. D.
D.
8.用二分法研究函数 的零点时,第一次经计算f (0)<0,f(0.5)>0,可得其中一个零点
的零点时,第一次经计算f (0)<0,f(0.5)>0,可得其中一个零点
 _ __,第二次应计算_ ___。
_ __,第二次应计算_ ___。
以上横线上应填的内容为 ( )
A.(0, 0.5), f( 0.25) B.(0, 1 ), f(0.25 )
C.(0. 5, 1) , f(0.75 ) D.(0, 0.5 ), f(0.125 )
9.已知函数 的导数为偶函数,则下面结论正确的是( )
的导数为偶函数,则下面结论正确的是( )
A. 是偶函数
B.
是偶函数
B. 是奇函数
是奇函数
C. 既有极大值,也有极小值 D.c=0
既有极大值,也有极小值 D.c=0
10. 已知 、
、 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,且
为两个不同的平面,且 ,
, ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
 .若
.若 ,则
,则
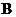 .若
.若 ,则
,则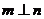
 .若
.若 ,
, 相交,则
相交,则 ,
, 也相交
也相交  .若
.若 ,
, 相交,则
相交,则 ,
, 也相交
也相交
 11. 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数
11. 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数 .则函数g(x)最大值为
A.0
B.2 C.1
D.4
.则函数g(x)最大值为
A.0
B.2 C.1
D.4
12下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程 =bx+a必过
=bx+a必过 ;
;
④曲线上的点与该点的坐标之间具有相关关系;
⑤在一个2×2列联表中,由计算得k2=13.079,则其两个变量间有关系的可能性是90%;
其中错误的个数是 ( ) A.1 B.2 C.3 D.4
本题可以参考两个分类变量x和y有关系的可信度表:
P(k2≥k)
0.5
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828

二、填空题(本大题共4小题,每小题5分,共20分)
13. 已知数列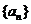 的通项公式
的通项公式 与前n项和公式
与前n项和公式 之间满足关系
之间满足关系 ,则
,则 =
=
14. 如图,在河对岸有移动公司的基站塔,为测塔高AB,选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点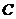 与
与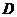 .测得
.测得


 并在点
并在点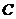 测得塔顶
测得塔顶 的仰角为
的仰角为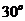 ,则塔高
,则塔高 =
(精确到0.01).
=
(精确到0.01).
 15. 已知函数y=f (x)的图象如图,则不等式f()>0的解集为
.
15. 已知函数y=f (x)的图象如图,则不等式f()>0的解集为
.
16. 在△ABC中,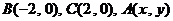 ,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
条件
方程
①△ABC周长为10
 :
:
②△ABC面积为10
 :
:
③△ABC中,∠A=90°
 :
:
则满足条件①、②、③的轨迹方程分别为
(用代号 、
、 、
、 填入)
填入)
三 、解答题(本大题共6小题共80分。解答应写出文字说明、证明过程或演算步骤)
17.(本题满分12分)
已知向量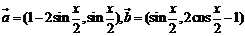 ,函数
,函数 。
。
(1)画出函数 在一个周期内的图像。
在一个周期内的图像。
(2)当 时,求
时,求 的最大值及
的最大值及 取得最大值时相应x取值的集合。
取得最大值时相应x取值的集合。
 18、(本题满分12分)
18、(本题满分12分)
正方体 ,
, ,
, 为棱
为棱 的中点,AC与BD交于点O.
的中点,AC与BD交于点O.
(1)求证:
(2)求证: ; (3)求三棱锥
; (3)求三棱锥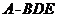 的体积.
的体积.
19.(本题满分12分) 甲、乙两人各抛掷一次正方体骰子(它们的六个面分别标有数字 ),设甲、乙所抛掷骰子朝上的面的点数分别为
),设甲、乙所抛掷骰子朝上的面的点数分别为 、
、 ,那么
,那么 。
。
(I)共有多少种不同的结果? 。
。
(II)请列出满足复数 的实部大于虚部的所有结果。
的实部大于虚部的所有结果。 。
。
(III)满足复数 的实部大于虚部的概率是多少?
的实部大于虚部的概率是多少?
20.(本小题满分12分)
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为 ,右顶点为
,右顶点为 ,设点A(1,1/2)。
,设点A(1,1/2)。
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点 的轨迹方程。
的轨迹方程。
21、(本小题满分12分)
已知函数 ,若
,若 在
在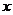 =1处的切线方程为
=1处的切线方程为 。
。
(1) 求 的解析式及单调区间;
的解析式及单调区间;
(2) 若对任意的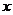

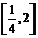 都有
都有 ≥
≥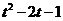 成立,求函数
成立,求函数 =
= 的最值。
的最值。
选考题(请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑。
22. (本小题满分10分)选修1―4:几何证明选讲
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD。
(1)求证:直线AB是⊙O的切线;
 (2)若tan∠CED=
(2)若tan∠CED= ,⊙O的半径为3,求OA的长。
,⊙O的半径为3,求OA的长。
23.(本小题满分10分)选修4-4坐标系与参数方程
若以原点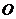 为极点,
为极点,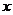 轴的正半轴为极轴,建立极坐标系,圆
轴的正半轴为极轴,建立极坐标系,圆 的极坐标方程为:
的极坐标方程为: .求圆的直角坐标方程。
.求圆的直角坐标方程。
24.(本小题满分10分)选修4-5 不等式选讲
.设函数
(1)
将 用分段函数表示;
用分段函数表示;
(2)
解不等式 <11
<11
石嘴山市2008―2009学年高考复习检测
数学试题(文)答案
一、
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
D
A
C
D
C
D
B
A
B
C
C
C
二、13
 .
14.23.55m 15.
.
14.23.55m 15. 16.
16.
三 、17.解.(1)

 +1
+1
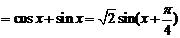 -----------------4分
-----------------4分
 图(略)
--------------------------------------8分
图(略)
--------------------------------------8分
(2)由(1)当且仅当 时,函数
时,函数 取得最大值,--------9分
取得最大值,--------9分
由

 。--------------10分
。--------------10分
 。12分
。12分
18. (1)(略证):连结 交于点Q,只需证
交于点Q,只需证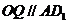 即可。---------3分
即可。---------3分
(2)证明:连结 ,则
,则 //
// ,∵
,∵ 是正方形,∴
是正方形,∴ .----4分
.----4分
∵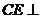 面
面 ,∴
,∴ .又
.又 ,∴
,∴ 面
面 .-----6分
.-----6分
∵ 面
面 ,∴
,∴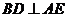 ,∴
,∴ . --------------------8分
. --------------------8分
(3)  . ----------------------------------------------------------9分
. ----------------------------------------------------------9分
 . ------------------------12分
. ------------------------12分
解: (I) 共有 种结果???????????????????????????????????????????????????????????????????????? 4分
种结果???????????????????????????????????????????????????????????????????????? 4分
(II) 若用 来表示两枚骰子向上的点数,满足复数
来表示两枚骰子向上的点数,满足复数 的实部大于虚部结果有:
的实部大于虚部结果有:
 ,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3),
,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3),
(5,3)(6,3),(5,4)(6,4),(6,5)共15种.????????????????????????????????????????? 8分
(III)满足复数 的实部大于虚部的概率是:P=
的实部大于虚部的概率是:P=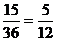 ?????????????????????????????? 12分
?????????????????????????????? 12分
20. 解(1)由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1.
---------------------------2分
,则半短轴b=1.
---------------------------2分
又椭圆的焦点在x轴上, ∴椭圆的标准方程为 -------------------------5分
-------------------------5分
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0), ------------------------6分
由  得
得 ------------------------8分
------------------------8分
由,点P在椭圆上,得 , ------------------------10分
, ------------------------10分
∴线段PA中点M的轨迹方程是 .
-------------------------12分
.
-------------------------12分
21. 解: 由已知得切点为 , 且
, 且 ----------1分
----------1分
(1)由题意可得 解得
解得 ,
--------------2分
,
--------------2分
故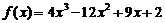
 ,
------------3分
,
------------3分
由 得:
得:  , 由
, 由 得:
得:  ------------4分
------------4分
由 得:
得: 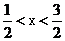 ,
------------5分
,
------------5分
 的单调增区间为
的单调增区间为 ,
, 的单调减区间为
的单调减区间为 ----6分
----6分
(2)由(1)可知 的极大值为
的极大值为 ,
------------------7分
,
------------------7分
又 ,
, ,
,
 在
在 上的最小值为2, ---------------8分
上的最小值为2, ---------------8分
由 对
对 恒成立, 则
恒成立, 则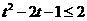 ,即
,即 ,解得
,解得 ,
---------------10分
,
---------------10分
而 , 故当
, 故当 时,
时, 最小值为
最小值为 ,当
,当 时,
时, 最大值为10
-------------12分
最大值为10
-------------12分
22. (1)证明:如图,连接OC,∵OA=OB,CA=CB ∴OC⊥AB
∴AB是⊙O的切线 …………………………………………4分
(2)解:∵ED是直径,∴∠ECD=90°∴∠E+∠EDC=90°
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
 ∴∠BCD=∠E
∴∠BCD=∠E
又∵∠CBD+∠EBC,∴△BCD∽△BEC
∴ ∴BC2=BD•BE
∴BC2=BD•BE
∵tan∠CED= ,∴
,∴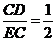
∵△BCD∽△BEC,
∴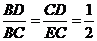
设BD=x,则BC=2
又BC2=BD•BE, ∴(2x)2=x•( x+6)
∴(2x)2=x•( x+6)
解得:x1=0,x2=2, ∵BD=x>0, ∴BD=2
∴OA=OB=BD+OD=3+2=5 ……………………………………10分
23.解:在方程 两边同乘以
两边同乘以 ,即
,即
 ,化为直角坐标方程得
,化为直角坐标方程得 ;
;
24.(1) ;---------6分;(2)
;---------6分;(2)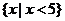 ----------------10分
----------------10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com