
2009年4月辽师大附中高三模拟试题及答案(理)
一、选择题:本大题共12小题:每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合 A = {x | x 2 + 2ax + 1 = 0} 的真子集只有一个,则 a 值的集合是( )
A.(-1,1) B. (-¥,-1]∪[1,+¥) C. {-1,1} D.{0}
2.函数 的反函数是( )
的反函数是( )
A. B.
B. C.
C.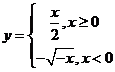

3.复数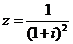 的虚部为( )
的虚部为( )
A. B.
B. C.
C. D.
D.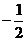
4.设 ,“
,“ ”是“曲线
”是“曲线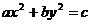 为椭圆”的( )
为椭圆”的( )
A.充分非必要条件 B.必要非充分条件 C.充分必要条件 D.既非充分又非必要条件
5.曲线 在原点处的切线方程为( )
在原点处的切线方程为( )
A.y = 1275x B.y = 502x C.y = 100x D.y = 50!x
6.从5门不同的文科课程和4门不同的理科课程中任选4门,组成一组综合高考科目组,要求这组科目中文、理科都有,则不同的选法种数为( )
A.2880
B.
7.已知双曲线的离心率e=2,且与椭圆 有相同的焦点,该双曲线的渐近线方程是( )
有相同的焦点,该双曲线的渐近线方程是( )
A. 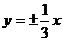 B.
B. C.
C.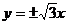 D.
D.
8.在空间直角坐标系 中,
中, 、
、 、
、  分别是
分别是 轴、
轴、 轴、
轴、 轴的方向向量,
轴的方向向量,
设 为非零向量,且
为非零向量,且 ,
,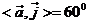 ,则
,则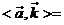 ( )
( )
A. B.
B. C.
C.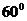 D.
D.
9.在线段[0,1]上任意投三个点,问由0至三点的三线段,能构成三角形与不能构成三角形这两个事件中哪一个事件的概率大。( )
A.一样大 B.能够成三角形概率大 C.不能够成三角形概率大 D.无法比较
 10.如图(1),正三棱台
10.如图(1),正三棱台 的上、下底面积之比为1:9,过
的上、下底面积之比为1:9,过 作平行于侧面
作平行于侧面 的截面
的截面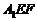 ,将棱台分成两个多面体,
,将棱台分成两个多面体,
则这两部分体积之比 等于( )
等于( )
A. B.
B. C.
C.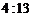 D.
D.
图(1)
11.若关于 的不等式组
的不等式组 的解集不是空集,则实数
的解集不是空集,则实数 的取值不可能是( )
的取值不可能是( )
A. B.
B. C.
C. D.
D.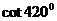
12.函数 的图象为C,且
的图象为C,且 有反函数,则将C( )
有反函数,则将C( )
A.向右向下各平移一个单位长度
B.向右向上各平移一个单位长度
C.向左向下各平移一个单位长度
D.向左向上各平移一个单位长度
后,再作关于直线y=x对称的图象,即为函数 的图象。
的图象。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中的横线上。
13.如图(2),该程序运行后输出的结果为 .

图(2)
14.一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次;则向上的数之积的数学期望是 ;
(从15---18四道题中选作两道)
15.已知圆O的 弦AB和CD相交于M,AB=10,且被M分成3:2的两段,如果CM=2,则CD= ;
16.设实数 满足
满足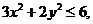 则
则 的 最大值是
;
的 最大值是
;
17.在极坐标系中,圆 的 圆心到直线
的 圆心到直线 的距离是
;
的距离是
;
18.设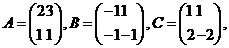 求
求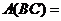
三、解答题:本大题共6道大题,19---23题每题12分,24题14分。
19.△ABC的三边为a,b,c,已知 ,且
,且 ,
,
求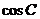 的值及三角形面积
的值及三角形面积 的最大值.
的最大值.
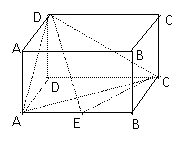
 20.如图(3),在长方体
20.如图(3),在长方体 中,
中, 点E在棱AB上移动.
点E在棱AB上移动.
(1)证明: ;
;
(2)若E为AB中点,求E到面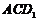 的距离;
的距离;
(3)AE等于何值时,二面角 的大小为
的大小为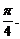
图(3)
⑴ 抽到的牌照号码恰好是沈阳市区的出租车的概率是多少?
21.辽宁省的地方汽车牌照号码为七位码,从左边起第一个位置是表示辽宁省的汉字“辽” ;第二个位置是代表城市的字母(如A代表沈阳市、B代表大连市等);后五个位置是汽车的编号,编号规则如下:按照汽车落户的先后顺序,从左边起由0 ~ 9这10个数字排成五位数字码;当五位数字码排满后,对之后落户的汽车,从左边起的第三、第四位置按除I、Q以外的24个英文字母依次编码,第五至第七位位置仍由数字0 ~ 9 依次编码,沈阳市区出租车的号码标志是第三位置的编码为T,例如“辽A TM
TM
⑵ 抽到的牌照号码在“辽A
⑶ 抽到的牌照号在“辽A GZ
GZ
22.设函数 分别在
分别在 处取得极小值、极大值.
处取得极小值、极大值.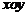 平面上点
平面上点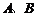 的坐标分别为
的坐标分别为 、
、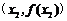 ,该平面上动点
,该平面上动点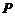 满足
满足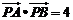 ,点
,点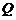 是点
是点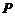 关于直线
关于直线 的对称点.求
的对称点.求
(I)求点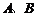 的坐标;
的坐标;
(II)求动点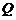 的轨迹方程.
的轨迹方程.
23. 已知数列 满足
满足 且对一切
且对一切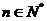 有
有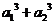 +……
+……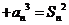 ,
,
(1)求证:对一切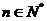 有
有
(2)求数列 的通项公式
的通项公式
(3)求证: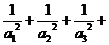 ……
……
24.已知倾斜角为 的直线
的直线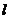 过点
过点 和点
和点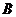 ,点
,点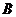 在第一象限,
在第一象限, 。
。
(1)求点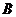 的坐标;
的坐标;
(2)若直线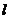 与双曲线
与双曲线 相交于
相交于 两点,且线段
两点,且线段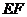 的中点
的中点
坐标为 ,求
,求 的值;
的值;
(3)对于平面上任一点 ,当点
,当点 在线段
在线段 上运动时,称
上运动时,称 的最小值为
的最小值为 与
与
线段 的距离。已知
的距离。已知 在
在 轴上运动,写出点
轴上运动,写出点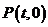 到线段
到线段 的距离
的距离
关于 的函数关系式。
的函数关系式。
参 考 答 案
第Ⅰ卷
题目
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
B
D
C
C
C
A
B
C
D
二、填空题:每小题4分,共16分。
13.63
14. 
15. 14
16. 
17.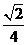 18.
18.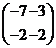
三、19.本题满分12分
解:  ,又由余弦定理得
,又由余弦定理得

 .
. ,
,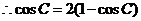 ,得
,得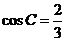 ,
,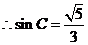 .又
.又 ,
,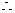
 .
.
当且仅当 时,等号成立.
时,等号成立.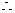
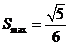 .
.
20.本题满分12分
 方法一
方法一
(I)证明:
(II)设点E到平面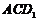 的距离为h,由题设可得
的距离为h,由题设可得
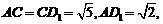
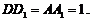 算得
算得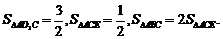 图(3)
图(3)
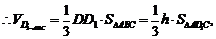 则
则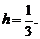
(III)过D作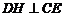 ,垂足为H,连
,垂足为H,连 则
则
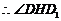 为二面角
为二面角 的平面角.
的平面角.
设 ,在直角
,在直角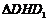 中,
中,
 在直角
在直角 中,
中,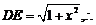 在直角
在直角 中,
中,
在直角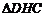 中,
中,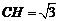 ,在直角
,在直角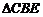 中,
中,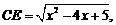
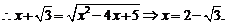
因为以上各步步步可逆,所以当 时,二面角
时,二面角 的大小为
的大小为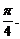
方法二:以DA,DC,DD1建立空间坐标系,设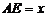 ,有
,有

(I)证明:因为 ,所以,
,所以,
(II)解:E是AB中点,有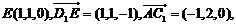
 ,设平面
,设平面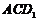 的法向量为
的法向量为 则
则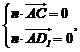 也即
也即 ,
,
得 ,从而
,从而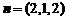 ,点E到平面
,点E到平面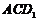 的距离
的距离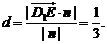
(III)设平面 的法向量为
的法向量为
 由
由 令
令 ,得
,得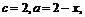
则 于是
于是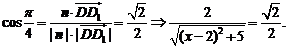
 (不合,舍去),
(不合,舍去),
即 时,二面角
时,二面角 的大小为
的大小为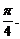
21. 本题满分12分
解:按照规则,沈阳市地方汽车的牌照号码共有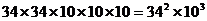 个。
个。
⑴ 沈阳市区出租车的牌照号码共有 个,故抽到的牌照号码恰好是出
个,故抽到的牌照号码恰好是出
租车的概率是
⑵ 牌照号码在“辽A
组成,其中最后一个数字为偶数的号码有 个,
个,
故所求概率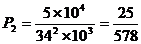
⑶ 牌照号码在“辽A GZ
GZ
E、 F、G中一个占据,共有17种可能,第四个位置有34种可能,
故号码在“辽A GZ
GZ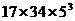 个,
个,
故所求概率为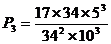
22. 本题满分12分
解析: (Ⅰ)令 解得
解得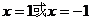 ;
;
当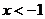 时,
时, , 当
, 当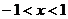 时,
时,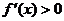 ,当
,当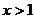 时,
时, 。
。
所以,函数在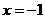 处取得极小值,在
处取得极小值,在 取得极大值,故
取得极大值,故 ,
, 。
。
所以, 点A、B的坐标为 。
。
(Ⅱ)
设 ,
,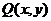 ,
,
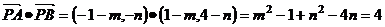 ,
,
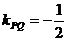 ,所以
,所以 。
。
又PQ的中点在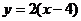 上,所以
上,所以 ,消去
,消去 得
得 。
。
23. 本题满分12分
解:(1)由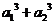 +……
+……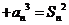 得
得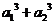 +……+
+……+
相减得:
 ?
?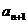

(2)由(1)知 得
得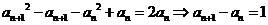 (
( ≥2)
≥2)
又 时
时 ,由
,由
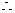

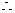
 为等差数列且
为等差数列且 =
=
(3)
24. 本题满分14分
解:(1)设 ,
,
 ,
, 
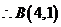
(2)设
由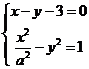 得
得 ,
,

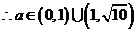
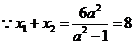 ,
,
(3)设线段 上任意一点
上任意一点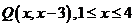


 当
当 时,即
时,即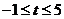 时,当
时,当 时,
时, ;
;
当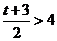 时,即
时,即 时,当
时,当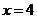 时,
时,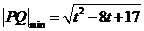 ;
;
当 时,即
时,即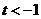 时,当
时,当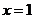 时,
时, 。
。
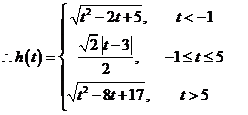
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com