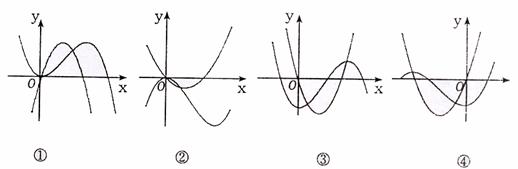
A.①② B.③④ C.①③ D.①④
试题详情
8.若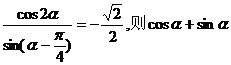 的值为 ( ) 的值为 ( ) 试题详情
试题详情
9.某单位要邀请10位教师中的6人参加一个研讨会,其中甲、乙两位教师不能同时参加,则邀请的不同方法有 ( ) A.84种 B.98种 C.112种 D.140种 试题详情
10.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为36π,那么这个正三棱柱的体积是 ( ) 试题详情
试题详情
11.连掷两次骰子分别得到点数是m、n,则向量(m、n)与向量(―1,1)的夹角θ<90°的概率是 ( ) 试题详情
试题详情
12.已知函数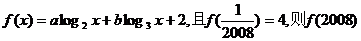 的值为 ( ) 的值为 ( ) A.2 B.0 C.―2 D.―4 试题详情
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上) 13.在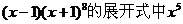 的系数是 。 的系数是 。 试题详情
14.在△ABC中,角A、B、C的对边分别是a,b,c,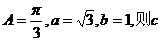 = 。 = 。 试题详情
15.在等式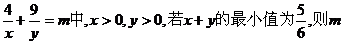 的值为 。 的值为 。 试题详情
16.设m、n是不同的直线,α、β、γ是不同的平面,有以下四个命题 试题详情
①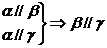 ② ②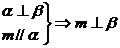 试题详情
③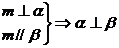 ④ ④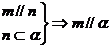 其中,真命题是
。 试题详情
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
试题详情
已知向量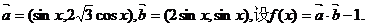 试题详情
(1)若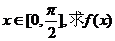 的值域; 的值域; 试题详情
(2)若函数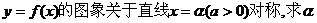 的最小值。 的最小值。 试题详情
18.(本题12分) 盒子里装有大小相同的球8个,其中三个1号球,三个2号球,两个3号球。第一次从盒子中先任取一个球,放回后第二次再任取一个球, (1)求第一次与第二次取到的球上的号码的和是4的概率; (2)记第一次与第二次取到的球的号码的积小于6的概率。 试题详情
19.(本题12分) 如图,在四棱锥P―ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB,PB的中点。
(1)求证:EF⊥CD; (2)求DB与平面DEF所成角的大小; (3)在平面PAD内是否存在一点G,使G在平面PCB上的射影为△PCB的外心,若存在,试确定点G的位置;若不存在,说明理由。 试题详情
|
|
|
试题详情
20.(本题满分12分)
|
试题详情
(1)求数列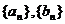 的通项公式; 的通项公式; 试题详情
(2)设数列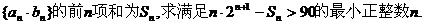 试题详情
试题详情
设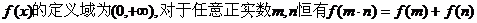 试题详情
且当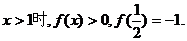 (1)求f(2)的值; 试题详情
(2)求证: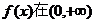 上是增函数; 上是增函数; 试题详情
(3)解关于x的不等式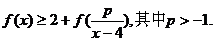 试题详情
试题详情
已知函数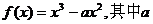 为正常数。 为正常数。 试题详情
(1)设当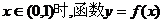 图象上任一点P处的切线的斜率为k,若 图象上任一点P处的切线的斜率为k,若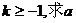 的取值范围; 的取值范围; 试题详情
(2)当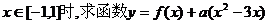 的最大值。 的最大值。 试题详情
一、选择题(本大题共12小题,每小题5分,共60分。 1―5 BBACB 6―10 ADCDD 11―12 AB 二、填空题(本大题共4小题,每小题6分,共16分, 13.14 14.2 15.30 16.①③ 三、解答题(本大题共6小题,共计76分) 17.解:(1) …………2分 …………2分 
(2)由题设, …………10分 …………10分  …………12分 …………12分
18.解:(1)记“第一次与第二次取到的球上的号码的和是4”为事件A,则  …………5分 …………5分
所以第一次与第二次取到的地球上的号码的和是4的概率 …………6分 …………6分 (2)记“第一次与第二次取到的上的号码的积不小于6”为事件B,则  …………11分 …………11分

19.解法一:(1)∵E,F分别是AB和PB的中点, ∴EF∥PA …………1分 又ABCD是正方形,∴CD⊥AD,…………2分 由PD⊥底面ABCD得CD⊥PD,CD⊥面PAD, ∴CD⊥PA,∴EF⊥CD。
…………4分 (2)设AB=a,则由PD⊥底面ABCD及ABCD是正方形可求得 

(3)在平面PAD内是存在一点G,使G在平面PCB 上的射影为△PCB的外心, G点位置是AD的中点。 …………9分 证明如下:由已知条件易证 Rt△PDG≌Rt△CDG≌Rt△BAG,…………10分 ∴GP=GB=GC,即点G到△PBC三顶点的距离相等。 ……11分 ∴G在平面PCB上的射影为△PCB的外心。 …………12分 解法二:以DA,DC,DP所在直线分别为x轴,y轴,z轴建立空间直角坐标系(如图)。

(1)  …………4分 …………4分
(2)设平面DEF的法向量为 
(3)假设存在点G满足题意 
20.解:(1)设 
(2) 
21.(1)令 …………1分 …………1分 而 …………2分 …………2分 (2)设 
(3)由 ∴不等式化为 …………6分 …………6分 由(2)已证 …………7分 …………7分 ①当 
②当 不成立,∴不等式的解集为 不成立,∴不等式的解集为 …………10分 …………10分 ③当 , ,  22.解:(1) 22.解:(1) …………1分 …………1分

(2)设 
①当 
②当 
| | | | | | | | | | | 
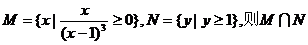 等于 ( )
等于 ( )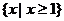 B.
B.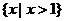
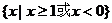 D.
D.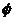
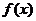 是定义在R上的奇函数,若
是定义在R上的奇函数,若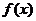 的最小正周期为3,
的最小正周期为3,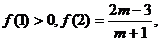 则m的取值范围是 ( )
则m的取值范围是 ( )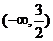 B.
B.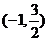
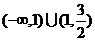 D.
D.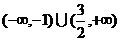
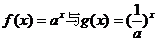 的图象 ( )
的图象 ( )