2．全反射条件：光线从光密介质射向光疏介质，且入射角大于或等于临界角．

1．全反射现象：光照射到两种介质界面上时，光线全部被反射回原介质的现象．

3．两种介质相比较，折射率较大的叫光密介质，折射率较小的叫光疏介质．

2．公式：，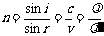

折射率总大于1．即n＞1．

1．定义：光从真空射入某种介质，入射角的正弦跟折射角的正弦之比，叫做介质的折射率．

注意：光从真空射入介质．

3．在折射现象中光路是可逆的．

2．折射定律：

(1)折射光线跟入射光线和法线在同一平面内

(2)折射光线和入射光线分居在法线的两侧

(3)入射角的正弦跟折射角的正弦值成正比

1．折射现象：光从一种介质进入另一种介质，传播方向发生改变的现象．

2．若入射光线不动，平面镜转过θ角，则反射光线转过2θ.

典型例题

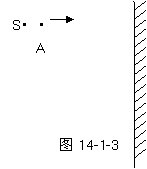例1．如图14-1-3所示，在A点有一个小球(可试作质点)，紧靠小球的左方有一个点光源S.现将小球从A点正对着竖直墙平抛出去，打到竖直墙之前，小球在点光源照射下的影子在墙上的运动是　 (　　 )　

A.匀速直线运动　　　　　　　

B.自由落体运动

C.变加速直线运动　　　　　　　　　

　D.匀减速直线运动

　解析：小球抛出后做平抛运动，时间t后水平位移是vt，竖直位移是h=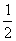gt²，根据相似形知识可以由比例求得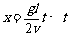，因此影子在墙上的运动是匀速运动,A项正确.

变式训练1.某人身高1.8 m，沿一直线以2 m/s的速度前进，其正前方离地面5 m高处有一盏路灯，试求人的影子在水平地面上的移动速度.

解析：如图图14-1-4所示，设人在时间t内由开始位置运动到G位置，人头部的影子由D点运动到C点

因为三角形ABC∽FGC，所以有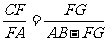

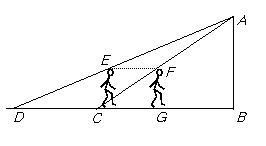又因为三角形ACD∽AFE，所以有　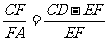　　 图14-1-4

由以上各式可以得到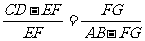　

即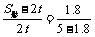　 解得S_影=3.125t　 .

可见影的速度为3.125m/s

例 2.如图14-1-5所示，用作图法确定人在镜前通过平面镜可看到AB完整像的范围.

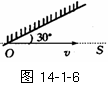
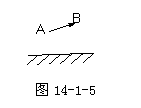解析：先根据对称性作出AB的像A^/B^/，分别作出A点、B点发出的光经平面镜反射后能射到的范围，再找到它们的公共区域(交集).就是能看到完整像的范围.

变式训练2.一个点光源S放在平面镜前，如图14-1-6所示．镜面跟水平方向成30⁰角，当光源S不动，平面镜以速度v沿水平OS方向向光源S平移．求光源S的像S^/的移动速度．

解析：利用物像对称性作出开始时光源S的像S^/．设在t时间里平面镜沿水平OS方向平移到S(即镜面与光源S重合)，则此时像与物重合，又由物像与镜面对称知：此过程像S^/的运动方向必沿着S^/S方向(垂直于镜面)．

　　 因为OS＝vt，所SS^/=2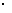(vtsin30⁰)＝vt

　　 故像的速率v^/v^/＝SS^//t=v

第2课时：光的折射　 全反射　 色散

基础过关

1．若平面镜不动，入射光线顺时针转过θ角，则反射光线逆时针转过θ角.