
题目列表(包括答案和解析)
6、如图将一块正方形纸片沿对角线折叠一次,然后在得到的三角菜的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )

A、 B、 C、 D、
5、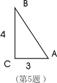 已知如图Rt△ABC中,∠C=90°,AC=3,BC=4,那么下列各式中,正确的是( )
已知如图Rt△ABC中,∠C=90°,AC=3,BC=4,那么下列各式中,正确的是( )
A、tanB=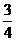 B、tanA=
B、tanA=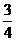
C、cosB=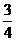 D、cosA=
D、cosA=
4、二次函数y=2(x–1)2-1的顶点坐标是( )
A (-1,-1) B (1,-1) C (-1,1) D (1,1)
3、如图Rt△ABC∽Rt△DEF,∠C=∠F=90°,点A与点D (第2题)
为对应点,∠B=60°,则∠E的度数( ) (第2题)
 A、30° B、45° C、60° D、90°
A、30° B、45° C、60° D、90°
2、如图:在平面直角坐标系中,点E的坐标是( )
A、(1,3) B、(3,1) C、(-1,3) D、(1,-3)
1、 4的平方根是( )
4的平方根是( )
 A、2 B、±2 C 、4 D、±4
A、2 B、±2 C 、4 D、±4
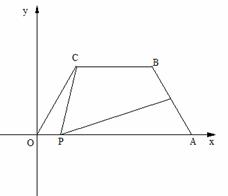
27.如图平面直角坐标中,四边形OABC是梯形,BC∥OA,OA=7,AB=OC=4,BC=3,
(1)求∠COA的度数;
(2)若P点在坐标轴上,且P、O、C三点构成等腰三角形,求P坐标;(只要写出坐标即可)
(3)在(2)中条件下,任取其中三点使经过该三点的图像是以y轴为对称轴的抛物线,称为最佳组合,求任取三点是最佳组合的概率.
(4)若有一个角是60°的三角板,60°角的顶点P在x轴上移动,三角板的60°角的一边经过C点,另一边与腰AB交与D ,问是否存在最大线段AD长度,如有求出最大值,且此时P点坐标,如没有,要说明理由.
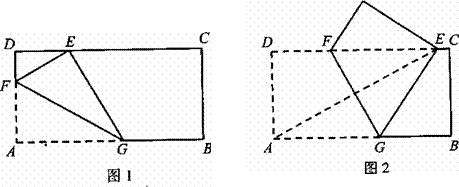
26.已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.
(1)如果折痕FG分别与AD、AB交于点F、G(如图1),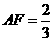 ,求DE的长;
,求DE的长;
(2)如果折痕FG分别与CD、AB交于点F、G(如图2),△AED的外接圆与直线BC相切,
求折痕FG的长.
25.已知:将一副三角板(Rt△DEF)如图1摆放,点E、A、D、B在一条直线上,且D是AB的中点,将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°).在旋转过程中,直线DE、AC相交于点M,直线DF、BC相交于点N,分别过点M、N作直线AB的垂线,垂足为G、H.
(1)当α=30°时(如图2),求证:AG=DH;
(2)当α=60°时(如图3),(1)中的结论是否成立?请写出你的结论,并说明理由;
(3)当0°<α<90°时(如图4),(1)中的结论是否成立?请写出你的结论,并说明理由.
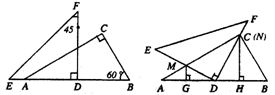
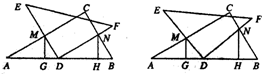
图1 图2 图3 图4
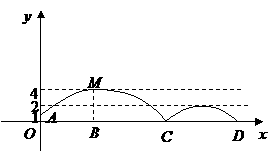
24.如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在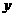 轴上),运动员乙在距
轴上),运动员乙在距 点6米的
点6米的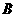 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点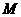 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点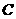 距守门员多少米?(取
距守门员多少米?(取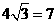 )
)
 (3)运动员乙要抢到第二个落点
(3)运动员乙要抢到第二个落点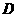 ,他应再向前跑多少米?(取
,他应再向前跑多少米?(取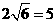 )
)
www.1230.org 初中数学资源网 收集整理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com